从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年投入将比上年减少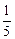 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加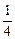 .
.
(1)设n年内(本年度为第一年)总投入为an万元,旅游业总收入为bn万元,写出an,bn的表达式;
(2)至少经过几年,旅游业的总收入才能超过总投入?
(本小题满分13分)如图,四面体ABCD中,O是BD的中点, ABD和
ABD和 BCD均为等边三角形,AB=2,
BCD均为等边三角形,AB=2, AC=
AC= 。
。
(1)求证:AO⊥平面BCD; (2)求二面角A—BC—D的大小;
(2)求二面角A—BC—D的大小;
(3)求O点到平面ACD的距离。
(本小题满分12分)设数列 的通项公式为
的通项公式为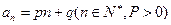 . 数列
. 数列 定义如下:对于正整数m,
定义如下:对于正整数m,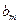 是使得不等式
是使得不等式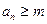 成立的所有n中的最小值.(1)若
成立的所有n中的最小值.(1)若 ,求
,求 ;(2)若
;(2)若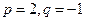 ,求数列
,求数列 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得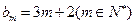 ?如果存在,求p和q的取值范围;如果不存在,请说明理由.
?如果存在,求p和q的取值范围;如果不存在,请说明理由.
(本小题满分12分)已知椭圆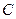 的中心在坐标原点,左顶点
的中心在坐标原点,左顶点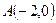 ,离心率
,离心率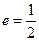 ,
,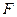 为右焦点,过焦点
为右焦点,过焦点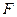 的直线交椭圆
的直线交椭圆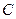 于
于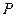 、
、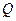 两点(不同于点
两点(不同于点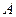 ).(1)求椭圆
).(1)求椭圆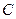 的方程;(2)当
的方程;(2)当 时,求直线PQ的方程;(3)判断
时,求直线PQ的方程;(3)判断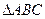 能否成为等边三角形,并说明理由.
能否成为等边三角形,并说明理由.
(本小题满分13分)设函数 .(1)求
.(1)求 的最小正周期(2)若函数
的最小正周期(2)若函数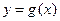 与
与 的图像关于直线
的图像关于直线 对称,求当
对称,求当 时
时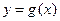 的最大值.
的最大值.
(本小题满分13分)设函数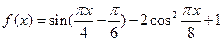 .(1)求
.(1)求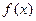 的最小正周期(2)若函数
的最小正周期(2)若函数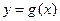 与
与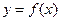 的图像关于直线
的图像关于直线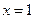 对称,求当
对称,求当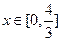 时
时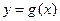 的最大值.
的最大值.