设a为实数,函数f(x)=ex-2x+2a,x∈R.
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当a>ln2-1且x>0时,ex>x2-2ax+1.
一座抛物线拱桥在某时刻水面的宽度为52米,拱顶距离水面6.5米.
(Ⅰ)建立如图所示的平面直角坐标系xOy,试求拱桥所在抛物线的方程;
(Ⅱ)若一竹排上有一4米宽6米高的大木箱,问此木排能否安全通过此桥?
设函数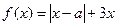 ,其中
,其中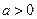 .
.
(Ⅰ)当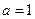 时,求不等式
时,求不等式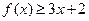 的解集;
的解集;
(Ⅱ)若不等式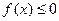 的解集为
的解集为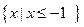 ,求a的值.
,求a的值.
(本小题满分10分)如图,在 △
△ 中,
中,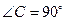 ,
, 平分
平分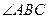 交
交 于点
于点 ,点
,点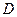 在
在 上,
上, .
.
(Ⅰ)求证: 是△
是△ 的外接圆的切线;
的外接圆的切线;
(Ⅱ)若 ,求
,求 的长.
的长.
(本小题满分10分)设 ,解关于
,解关于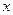 的不等式:
的不等式:
(本小题满分8分)在直角坐标系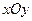 中,直线
中,直线 的参数方程为
的参数方程为
(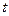 为参数).在极坐标系(与直角坐标系
为参数).在极坐标系(与直角坐标系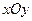 取相同的长度单位,且以原点
取相同的长度单位,且以原点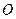 为极点,以
为极点,以 轴正半轴为极轴)中,圆
轴正半轴为极轴)中,圆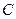 的方程为
的方程为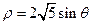 .
.
(I)求圆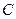 的参数方程;
的参数方程;
(II)设圆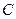 与直线
与直线 交于点
交于点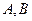 ,求弦长
,求弦长