如图所示，一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场，它刚好贴着下板右边缘飞出．已知匀强电场两极板长为L，间距为d，粒子的重力忽略不计。求：
（1）如果带电粒子的速度变为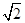
v0，则离开电场时，沿场强方向偏转的距离为多少？
（2）如果带电粒子的速度变为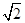v0，板长L不变，当它的竖直位移仍为d时，它的水平总位移为多少？
如图所示，一辆汽车从A点开始爬坡，坡与水平面间的夹角为300，在牵引力不变的条件下行驶45 m的坡路到达B点时，司机立即关掉油门，以后汽车又向前滑行15 m停在C点，汽车的质量为5×103 kg，行驶中受到的摩擦阻力是车重的0.25倍，取g＝10 m/s2，求汽车的牵引力做的功和它经过B点时的速率．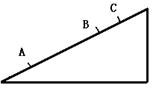
做匀加速直线运动的物体途中依次经过A、B、C三点，已知AB=BC，AB段和BC段的平均速度分别为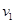
=3m/s、
=6m/s，则
（1）物体经B点时的瞬时速度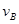
为多大？
（2）若物体运动的加速度a=2m/s2,试求AC的距离。
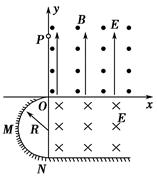
(14分)如下图，竖直平面坐标系
的第一象限，有垂直面向外的水平匀强磁场和竖直向上的匀强电场，大小分别为B和E；第四象限有垂直面向里的水平匀强电场,大小也为
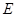；第三象限内有一绝缘光滑竖直放置的半径为
的半圆轨道,轨道最高点与坐标原点
相切,最低点与绝缘光滑水平面相切于
.一质量为
的带电小球从
轴上(
)的
点沿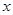
轴正方向进入第一象限后做圆周运动,恰好通过坐标原点,且水平切入半圆轨道并沿轨道内侧运动,过点水平进入第四象限,并在电场中运动(已知重力加速度为
).
(1)判断小球的带电性质并求出其所带电荷量；
(2)点距坐标原点至少多高；
(3)若该小球以满足(2)中
最小值的位置和对应速度进入第一象限,通过点开始计时,经时间
小球距坐标原点的距离
为多远？
(10分).如图所示,金属杆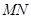
,在竖直平面内贴着光滑平行金属导轨下滑,导轨的间距
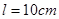,导轨上端接有
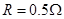的电阻,导轨与金属杆的电阻不计,整个装置处于
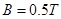的水平匀强磁场中,磁场方向垂直于导轨平面.当金属杆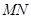下滑时,每秒钟有
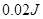的重力势能减少,求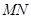杆下滑的速度的大小(不计空气阻力).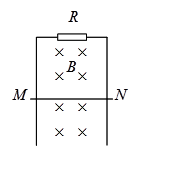
(10分).质量为
的物体在一恒定水平外力
作用下,沿水平面作直线运动,其速度与时间关系图像如图所示.
,试求:
(1)恒力的大小;
(2)地面动摩擦因数
.