图18甲所示，平行金属板PQ、MN水平地固定在地面上方的空间，金属板长 l=20cm，两板间距d=10cm，两板间的电压UMP=100V。在距金属板M端左下方某位置有一粒子源A，从粒子源竖直向上连续发射速度相同的带电粒子，射出的带电粒子在空间通过一垂直于纸面向里的磁感应强度B=0.20T的圆形区域匀强磁场(图中未画出)后，恰好从金属板 PQ左端的下边缘水平进入两金属板间，带电粒子在电场力作用下恰好从金属板MN的右边缘飞出。已知带电粒子的比荷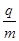
=2.0×106C/kg，粒子重力不计，计算结果保留两位有效数字。求：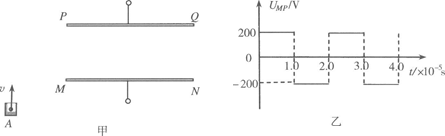
(1)带电粒子射人电场时的速度大小；
(2)圆形匀强磁场区域的最小半径；
(3)若两金属板间改加如图乙所示的电压，在哪些时刻进入两金属板间的带电粒子不碰到极板而能够飞出两板间。
如图所示，薄平板A长L=1m，质量为
kg，放在水平地面上，在A上最右端处放一个质量
kg的小物体B，已知A与B之间的动摩擦因数
，A、B两物体与桌面间的动摩擦因数均为
，最初系统静止。现在对板A右端施一大小为F=36N的水平恒力作用并开始计时，则：（取
m/s2）
（1）A、B两物体分离时F的功率P；
（2）在t=5s时B与平板A左端的距离x；
（3）在t=5s内平板A克服摩擦力做的功W。
以v0=20m/s的初速度，从地面竖直向上抛出一质量为m=5kg物体，物体落回地面时的速度大小为v=10m/s。如果物体在运动过程中所受阻力的大小不变，且和地面碰后不再反弹 （以地面为重力零势能面，g=10m/s2），求：
（1）物体运动过程中所受阻力的大小；
（2）物体在离地面多高处，物体的动能与重力势能相等。
火箭发射卫星的开始阶段是竖直升空，设向上的加速度为a=5m/s2，卫星中用弹簧秤悬挂一个质量m=9kg的物体。当卫星升空到某高处时，弹簧秤的示数为85N，那么此时卫星距地面的高度是多少千米（地球半径取R=6400km，g=10m/s2）？
某同学利用DIS实验系统研究一定质量理想气体的状态变化，实验后计算机屏幕显示如下的
图象。已知在状态
时气体的体积
，求：
①气体在状态
的压强；②气体在状态
的体积。
如图（a）所示，平行金属板
和
间的距离为
，现在、板上加上如图（b）所示的方波形电压，
=0时板比板的电势高，电压的正向值为
，反向值也为，现有由质量为
的带正电且电荷量为
的粒子组成的粒子束，从
的中点
以平行于金属板方向
的速度
不断射入，所有粒子不会撞到金属板且在间的飞行时间均为
，不计重力影响。试求：
（1）粒子射出电场时的速度大小及方向；
（2）粒子打出电场时位置离
点的距离范围；
（3）若要使打出电场的粒子经某一垂直纸面的圆形区域匀强磁场偏转后，都能到达圆形磁场边界的同一个点，而便于再收集，则磁场区域的最小半径和相应的磁感强度是多大？