探究:已知平行四边形ABCD的面积为100,M是AB所在直线上的一点
(1)如图1:当点M与B重合时,S△DCM =________;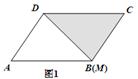
(2)如图2:当点M与B与A均不重合时,S△DCM =________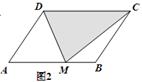
(3)如图3:当点M在AB(或BA)的延长线上时,S△DCM =________
推广:平行四边形ABCD的面积为a,E、F为两边DC、BC延长线上两点,连接DF、AF、AE、BE.求出图4中阴影部分的面积,并简要说明理由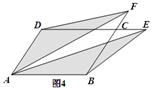
应用:如图5是某广场的一平行四边形绿地ABCD,PQ、MN分别平行DC、AD,PQ、MN交于O点,其中S四边形AM OP=300m2,S四边形MBQO=400m2,S四边形NCQO=700m2.现进行绿地改造,在绿地内部做一个三角形区域MQD,连接DM、QD、QM,(图中阴影部分)种植不同的花草,求三角形DMQ区域的面积.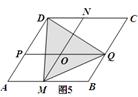
已知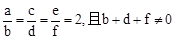 .
.
(1)求 的值;(2)若
的值;(2)若 ,求
,求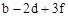 的值.
的值.
如图,已知△ABC中,BD、CE是高,F是BC中点,连接DE、EF和DF.
(1)求证:△DEF是等腰三角形;
(2)若∠A=45°,试判断△DEF的形状,并说明理由;
(3)若∠A:∠DFE=5:2,BC=4,求△DEF的面积.
如图,已知△ABC中,∠B=48°,∠C=62°,点E、点F分别在边AB和边AC上,将把△AEF沿EF折叠得△DEF,点D正好落在边BC上(点D不与点B.点C重合).
(1)如图1,若BD=BE,则△CDF是否为等腰三角形?请说明理由.
(2)△BDE、△CDF能否同时为等腰三角形?若能,请画出所有可能的图形,并直接指出△BDE、△CDF的三个内角度数;若不能,请说明理由.
华盛印染厂生产某种产品,每件产品出厂价为30元,成本价为20元(不含污水处理部分费用).在生产过程中,平均每生产1件产品就有0.5立方米污水排出,所以为了净化环境,工厂设计了两种对污水进行处理的方案并准备实施.
方案一:工厂污水先净化处理后再排出,每处理1立方米污水所用的原料费用为2元,并且每月排污设备损耗等其它各项开支为27000元.
方案二:将污水排放到污水处理厂统一处理,每处理1立方米污水需付8元排污费.
(1)若实施方案一,为了确保印染厂有利润,则每月的产量应该满足怎样的条件?
(2)你认为该工厂应如何选择污水处理方案?
求证:两条直线被第三条直线所截,如果同旁内角的角平分线互相垂直, 那么这两条直线互相平行.