某学校环保志愿者协会对该市城区的空气质量进行调查,从全年365天中随机抽取了80天的空气质量指数(AQI)数据,绘制出三幅不完整的统计图表.请根据图表中提供的信息解答下列问题:
AQI指数 |
质量等级 |
天数(天) |
|
优 |
m |
|
良 |
44 |
|
轻度污染 |
n |
|
中度污染 |
4 |
|
重度污染 |
2 |
300以上 |
严重污染 |
2 |
(1 )统计表中m= ,n= .扇形统计图中,空气质量等级为“良”的天数占 %;
(2)补全条形统计图,并通过计算估计该市城区全年空气质量等级为“优”和“良”的天数共多少天?
(3)据调查,严重污染的2天发生在春节期间,燃放烟花爆竹成为空气污染的一个重要原因,据此,请你提出一条合理化建议.

如图,已知点 、 、 、 在同一条直线上, , , .求证: .

如图,已知抛物线 的图象经过点 , ,与 轴交于点 ,抛物线的顶点为 ,对称轴与 轴相交于点 ,连接 .
(1)求抛物线的解析式.
(2)若点 在直线 上,当 时,求点 的坐标.
(3)在(2)的条件下,作 轴于 ,点 为 轴上一动点, 为直线 上一动点, 为抛物线上一动点,当以点 , , , 四点为顶点的四边形为正方形时,求点 的坐标.

如图, 是 的直径,点 , 在 上, ,点 在 的延长线上, .
(1)求证: 是 的切线;
(2)若 , ,求 的半径长.

校园超市以4元 件购进某物品,为制定该物品合理的销售价格,对该物品进行试销调查.发现每天调整不同的销售价,其销售总金额为定值,其中某天该物品的售价为6元 件时,销售量为50件.
(1)设售价为 元 件时,销售量为 件.请写出 与 的函数关系式;
(2)若超市考虑学生的消费实际,计划将该物品每天的销售利润定为60元,则该物品的售价应定为多少元 件?
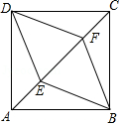
如图, , 是正方形 的对角线 上的两点,且 .
(1)求证:四边形 是菱形;
(2)若正方形边长为4, ,求菱形 的面积.