某校为了解决学生停车难的问题,打算新建一个自行车车棚,图1是车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一部分,其展开图是矩形.图2是车棚顶部的截面示意图,弧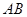 所在圆的圆心为
所在圆的圆心为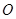 ,半径
,半径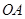 为3米.
为3米.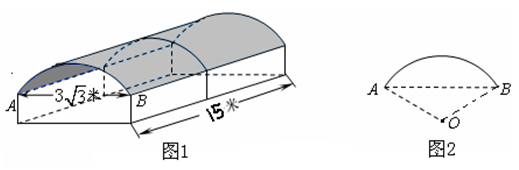
(1)求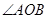 的度数;
的度数;
(2)学校准备用某种材料制作车棚顶部,请你算一算,需该种材料多少平方米?(不考虑接缝等因素,结果精确到1平方米).
(第2小题的参考数据: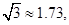
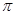 取3.14)
取3.14)
已知抛物线与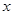 交于A(-1,0)、B(3,0)两点,与
交于A(-1,0)、B(3,0)两点,与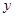 轴交于点C(0,3),求抛物线的解析式;
轴交于点C(0,3),求抛物线的解析式;
已知,如图所示抛物线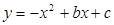 与x的两个交点分别为A(1,0),B(3,0)。
与x的两个交点分别为A(1,0),B(3,0)。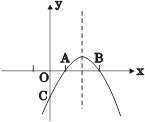
(1)求抛物线的解析式;
(2)设点P在该抛物线上滑动,且满足条件S△PAB = 1这样的点P有几个?并求出所有点P 的坐标;
(3)设抛物线交y轴于点C,问该抛物线对称轴上是否存在点M,使得△MAC的周长最小.若存在,求出点M的坐标;若不存在,请说明理由.
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,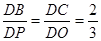 .
.
(1)求证:直线PB是⊙O的切线;
(2)求cos∠BCA的值.
某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册0.4元.小军经常来该店租书,若每月租书数量为x册.
(1)写出零星租书方式应付金额y1(元)与租书数量x(册)之间的函数关系式;
(2)写出会员卡租书方式应付金额y2(元 )与租书数量x(册)之间的函数关系式;
(3)小军选取哪种租书方式更合算?
如图所示,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点。已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE= m。求点B到地面的垂直距离BC.
m。求点B到地面的垂直距离BC.