如图1,在正方形ABCD中,AB=1,点E在AB延长线上,联结CE、DE,DE交边BC于点F,设BE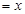 ,CF
,CF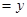 .
.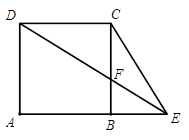
图1
(1)求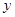 关于
关于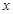 的函数解析式,并写出
的函数解析式,并写出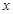 的取值范围;
的取值范围;
(2)如图2,对角线AC、BD的交点记作O,直线OF交线段CE于点G,求证: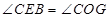 ;
;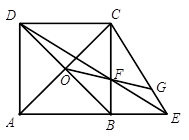
图2
(3)在(2)的条件下,当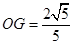 时,求
时,求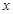 的值.
的值.
某校有2000名学生,为了解全校学生的上学方式,该校数学兴趣小组在全校随机抽取了150名学生进行抽样调查。整体样本数据,得到下列图表: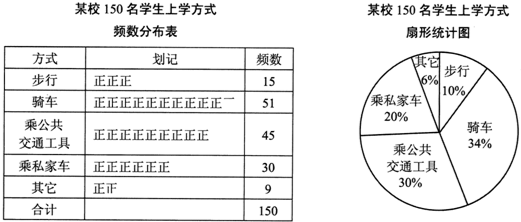
(1)理解画线语句的含义,回答问题:如果150名学生全部在同一个年级抽取,这样的抽样是否合理?请说明理由:
(2)根据抽样调查的结果,将估计出的全校2000名学生上学方式的情况绘制成条形统计图;
(3)该校数学兴趣小组结合调查获取的信息,向学校提出了一些建议。如:骑车上学的学生数约占全校的34%,建议学校合理安排自行车停车场地。请你结合上述统计的全过程,再提出一条合理化建议:。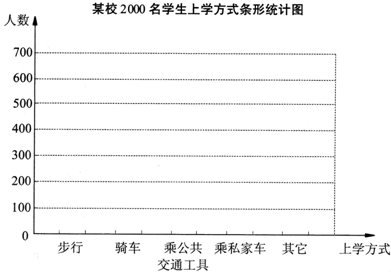
(1)一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各一个,这些球除颜色外都相同。求下列事件的概率:
①搅匀后从中任意摸出1个球,恰好是红球;
②搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,两次都是红球;
(2)某次考试有6道选择题,每道题所给出的4个选项中,恰有一项是正确的,如果小明从每道题的4个选项中随机地选择1个,那么他6道选择题全部选择正确的概率是
A.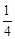 |
B.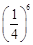 |
C. |
D.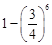 |
如图,在四边形ABCD中,AB=BC,对角线BD平分ÐABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。
(1)求证:ÐADB=ÐCDB;
(2)若ÐADC=90°,求证:四边形MPND是正方形。
解方程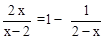 。
。
化简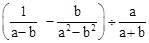 。
。