如图，抛物线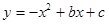
的顶点为Q，与
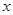轴交于A(-1，0)、B(5， 0)两点，与
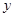轴交于C点．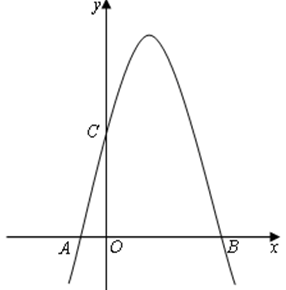
(1)直接写出抛物线的解析式及其顶点Q的坐标；
(2)在该抛物线的对称轴上求一点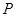
,使得△
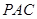的周长最小.请在图中画出点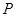的位置，并求点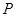的坐标．
解方程：3x－2＝1－2(x＋1)
化简并求值：9x+6x2－3(x－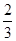
x2) ，其中x=－2．
甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0．5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．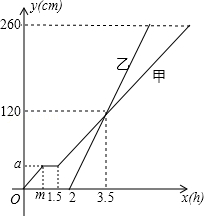
（1）求出图中m，a的值；
（2）求出甲车行驶路程y（km）与时间x（h）的函数解析式，并写出相应的x的取值范围；
（3）当乙车行驶多长时间时，两车恰好相距50km．
广安某水果点计划购进甲、乙两种新出产的水果共140千克，这两种水果的进价、售价如表所示：
| 进价（元/千克） |
售价（元/千克） |
|
| 甲种 |
5 |
8 |
| 9 |
13 |
（1）若该水果店预计进货款为1000元，则这两种水果各购进多少千克？
（2）若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍，应怎样安排进货才能使水果点在销售完这批水果时获利最多？此时利润为多少元？
（本题10分）如图，
中，AD是高，E、F分别是AB、AC的中点。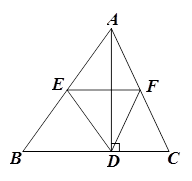
（1）若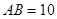
，
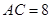，求四边形AEDF的周长；
（2）求证：EF垂直平分AD。