如图,已知点C、D在以O为圆心,AB为直径的半圆上,且OC⊥BD于点M,CF⊥AB于点F交BD于点E,BD=8,CM=2.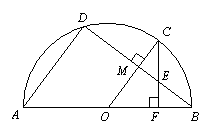
(1)求⊙O的半径;
(2)求证:CE=BE.
定义:点 是 内部或边上的点(顶点除外),在 , , 中,若至少有一个三角形与 相似,则称点 是 的自相似点.
例如:如图1,点 在 的内部, , ,则 ,故点 是 的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点 是曲线 上的任意一点,点 是 轴正半轴上的任意一点.
(1)如图2,点 是 上一点, ,试说明点 是 的自相似点;当点 的坐标是 , ,点 的坐标是 , 时,求点 的坐标;
(2)如图3,当点 的坐标是 ,点 的坐标是 时,求 的自相似点的坐标;
(3)是否存在点 和点 ,使 无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.

已知函数 的图象与 轴有两个公共点.
(1)求 的取值范围,并写出当 取值范围内取最大整数时函数的解析式;
(2)题(1)中求得的函数记为 .
①当 时, 的取值范围是 ,求 的值;
②函数 的图象由函数 的图象平移得到,其顶点 落在以原点为圆心,半径为 的圆内或圆上.设函数 的图象顶点为 ,求点 与点 距离最大时函数 的解析式.
实验探究:
(1)如图1,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展开;再一次折叠纸片,使点 落在 上,并使折痕经过点 ,得到折痕 ,同时得到线段 , .请你观察图1,猜想 的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片 剪下,如图2.折叠该纸片,探究 与 的数量关系.写出折叠方案,并结合方案证明你的结论.

如图,已知 的直径 ,弦 , 是 的中点,过点 作 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)求 的长.

某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量 (单位:个)与销售单价 (单位:元)有如下关系: .
设这种双肩包每天的销售利润为 元.
(1)求 与 之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?