如图所示,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.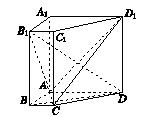
(1)证明:AC⊥B1D;
(2)求直线B1C1与平面ACD1所成角的正弦值.
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为
米,高为
米,体积为
立方米.假设建造成本仅与表面积有关,侧面积的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12000
元(π为圆周率).
(1)将
表示成
的函数
,并求该函数的定义域;
(2)讨论函数
的单调性,并确定
和
为何值时该蓄水池的体积最大.
如图,四棱锥
中,
底面
,
,
,
.
(1)求证:
平面
;
(2)若侧棱
上的点
满足
,求三棱锥
的体积.
在
中,内角
的对边分别是
,且
.
(1)求
;
(2)设
,
为
的面积,求
的最大值,并指出此时
的最值.
从某居民区随机抽取10个家庭,获得第
个家庭的月收入
(单位:千元)与月储蓄
(单位:千元)的数据资料,算得
.(1)求家庭的月储蓄
对月收入
的线性回归方程
;
(2)判断变量
与
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程
中,
,其中
为样本平均值,线性回归方程也可写为
.
设数列
满足:
.
(1)求
的通项公式及前
项和
;
(2)已知
是等差数列,
为前
项和,且
,求
.