若集合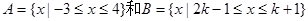 ,其中
,其中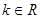 .
.
(1)当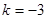 时,求集合
时,求集合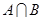 ;
;
(2)当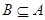 时,求实数
时,求实数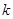 的取值范围.
的取值范围.
(本小题满分14分)
设Sn表示数列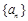 的前n项和.
的前n项和.
(Ⅰ)若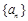 为等差数列,推导Sn的计算公式;
为等差数列,推导Sn的计算公式;
(Ⅱ)若 , 且对所有正整数n, 有
, 且对所有正整数n, 有 .判断
.判断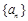 是否为等比数列.
是否为等比数列.
(本小题满分14分)
长方体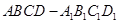 中,
中, ,
,  ,
, 是底面对角线的交点。
是底面对角线的交点。
(Ⅰ)求证: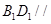 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥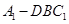 的体积。
的体积。
(本小题满分12分)
某人有3枚钥匙,其中只有一枚房门钥匙,但忘记了开房门的是哪一枚,于是,他逐枚不重复地试开,问:
(Ⅰ)恰好第三次打开房门锁的概率是多少?
(Ⅱ)两次内打开房门的概率是多少?
(本小题满分12分)
已知 ,且
,且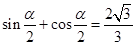 .
.
(Ⅰ)求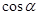 的值;
的值;
(Ⅱ)若 ,
, ,求
,求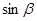 的值.[来源
的值.[来源
(本小题满分14分)
设函数 .
.
(1)若函数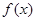 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数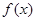 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.