某医药研究所开发一种新药,据监测,如果成人按规定剂量服用该药,服药后每毫升血液中的含药量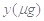 与服药后的时间
与服药后的时间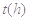 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中 是线段,曲线段
是线段,曲线段 是函数
是函数
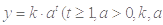 是常数
是常数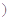 的图象.
的图象.
(1)写出服药后每毫升血液中含药量 关于时间
关于时间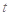 的函数关系式;
的函数关系式;
(2)据测定:每毫升血液中含药量不少于 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?
(3)若按(2)中的最迟时间服用第二次药,则第二次服药后再过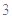
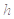 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少 ?
?
甲设计了一个摸奖游戏,在一个口袋中装有同样大小的10个球,分别标有数字0,1,2,……9这十个数字,摸奖者交5元钱可参加一回摸球活动,一回摸球活动的规则是:摸奖者在摸球前先随机确定(预报)3个数字,然后开始在袋中不放回地摸3次球,每次摸一个,摸得3个球的数字与预先所报数字均不相同的奖1元,有1个数字相同的奖2元,2个数字相同的奖10元,3个数字相同的奖50元,设ξ为摸奖者一回所得奖金数,求ξ的分布列和摸奖人获利的数学期望.
在 中,
中,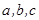 分别是角A、B、C的对边,且满足:
分别是角A、B、C的对边,且满足: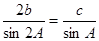 .
.
(I)求角C;
(II)求函数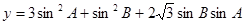 的单调减区间和取值范围.
的单调减区间和取值范围.
已知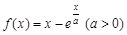 .
.
(Ⅰ)判断曲线 在
在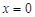 的切线能否与曲线
的切线能否与曲线 相切?并说明理由;
相切?并说明理由;
(Ⅱ)若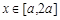 求
求 的最大值;
的最大值;
(Ⅲ)若 ,求证:
,求证: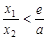 .
.
已知圆O: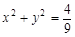 ,直线l:
,直线l: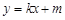 与椭圆C:
与椭圆C: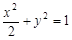 相交于P、Q两点,O为原点.
相交于P、Q两点,O为原点.
(Ⅰ)若直线l过椭圆C的左焦点,且与圆O交于A、B两点,且 ,求直线l的方程;
,求直线l的方程;
(Ⅱ)如图,若 重心恰好在圆上,求m的取值范围.
重心恰好在圆上,求m的取值范围.
如图,在直角梯形ABCD中, ,
,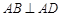 ,且
,且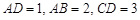 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面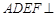 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.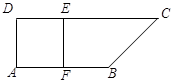
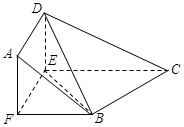
(Ⅰ)求证: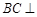 平面BDE;
平面BDE;
(Ⅱ)求平面BCEF与平面ABD所成二面角(锐角)的大小.