“健身弹跳球”是最近在少年儿童中特别流行的一项健身益智器材，少年儿童在玩弹跳球时如图一要双脚站在弹跳球的水平跳板上，用力向下压弹跳球，形变的弹跳球能和人一起跳离地面。该过程简化为：一、形变弹跳球向上恢复原状，二、人和弹跳球竖直上升，假设小孩质量为m，人和球一起以速度大小v0离开地面还能竖直上升h高（上升过程小孩只受重力作用），地球半径为R，引力恒量为G，
求（1）、此次起跳过程弹跳球对小孩做多少功？（2）地球的质量为多少？
如图质量为m=0.2kg的小球固定在长为L=0.9m的轻杆一端，杆可绕O点的水平转轴在竖直平面内转动，g=10m/s2，求：
（1）小球在最高点的速度v1为多大时，球对杆的作用力为0？
（2）当小球在最高点的速度v2=6m/s时，球对杆的作用力和方向。
有一辆质量为800kg的小汽车驶上圆弧半径为50m的拱桥。
（1）汽车到达桥顶时速度为5m/s，汽车对桥的压力是多大？
（2）汽车以多大速度经过桥顶时恰好对桥没有压力而腾空？
一个质子由两个u夸克和一个d夸克组成。一个夸克的质量是7.1×10-30kg，求两个夸克相距1.0×10-16m时的万有引力。
地球可以看做一个半径为6.4×106m的球体，位于赤道的物体，随地球自转做匀速圆周运动的角速度为多大？线速度为多大？
如图所示，一个挂在丝线下端带正电的小球B，静止在图示位置。若固定的带正电小球A的电荷量为Q，B球的质量为m，带电荷量为q，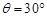
，A和B在同一条水平线上，均可视为点电荷，整个装置处于真空中。试求A、B两球间的距离r。已知静电力常量为k。