设等比数列 的首项为
的首项为 ,公比为
,公比为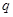 (
(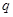 为正整数),且满足
为正整数),且满足 是
是 与
与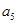 的等差中项;数列
的等差中项;数列 满足
满足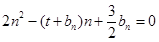 (
(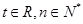 ).
).
(1)求数列 的通项公式;
的通项公式;
(2)试确定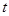 的值,使得数列
的值,使得数列 为等差数列;
为等差数列;
(3)当 为等差数列时,对每个正整数
为等差数列时,对每个正整数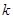 ,在
,在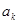 与
与 之间插入
之间插入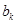 个2,得到一个新数列
个2,得到一个新数列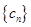 . 设
. 设 是数列
是数列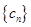 的前
的前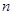 项和,试求满足
项和,试求满足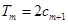 的所有正整数
的所有正整数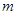 .
.
.(本小题满分12分)
(1)设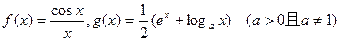 ,求
,求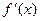 和
和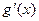 ;
;
(2)设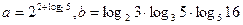 ,求
,求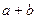 的值。
的值。
已知函数 ,其中
,其中 为大于零的常数.
为大于零的常数.
(Ⅰ)若曲线 在点(1,
在点(1, )处的切线与直线
)处的切线与直线 平行,求
平行,求 的值;
的值;
(Ⅱ)求函数 在区间[1,2]上的最小值.
在区间[1,2]上的最小值.
已知数列 满足
满足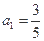 ,
,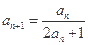 ,
,
(Ⅰ)计算出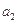 、
、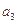 、
、 ;
;
(Ⅱ)猜想数列 通项公式
通项公式
 ,并
,并 用数学归纳法进行证明.
用数学归纳法进行证明.
在直角坐标系 中,以O为极点,
中,以O为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线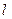 的极坐标方程为
的极坐标方程为 .圆O的参数方程为
.圆O的参数方程为 ,(
,(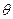 为参数,
为参数, )
)
(1)求 圆心的极坐标;
圆心的极坐标;
(2)当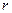 为何值时,圆O上的点到直线
为何值时,圆O上的点到直线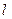 的最大距离为3.
的最大距离为3.
今有甲、乙两个篮球队进行比赛,比赛采用7局4胜制.假设甲、乙两队在每场比赛中获胜的概率都是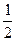 .并记需要比赛的场数为ξ.
.并记需要比赛的场数为ξ.
(Ⅰ)求ξ大于5的概率;(Ⅱ)求ξ的分布列与数学期望.