如图:A、B两城相距100 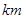 ,某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气.已知D地距A城
,某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气.已知D地距A城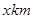 ,为保证城市安全,天燃气站距两城市的距离均不得少于10
,为保证城市安全,天燃气站距两城市的距离均不得少于10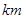 .已知建设费用
.已知建设费用 (万元)与A、B两地的供气距离(
(万元)与A、B两地的供气距离(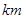 )的平方和成正比,当天燃气站D距A城的距离为40
)的平方和成正比,当天燃气站D距A城的距离为40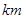 时, 建费用为1300万元.(供气距离指天燃气站距到城市的距离)
时, 建费用为1300万元.(供气距离指天燃气站距到城市的距离)
(1)把建设费用 (万元)表示成供气距离
(万元)表示成供气距离 (
(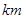 )的函数,并求定义域;
)的函数,并求定义域;
(2)天燃气供气站建在距A城多远,才能使建设供气费用最小,最小费用是多少?
汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆);
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
按类型用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(Ⅰ)求z的值;
(Ⅱ)用分层抽样的方法在C类轿车中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(Ⅲ)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8辆轿车的得分看成一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率
已知函数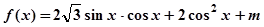 在区间
在区间 上的最大值为2
上的最大值为2 .
.
(1)求常数 的值;
的值;
(2)在 中,角
中,角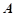 ,
, ,
, 所对的边是
所对的边是 ,
,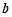 ,
, ,若
,若 ,
, ,
, 面积为
面积为 .求边长
.求边长 .
.
(满分15分)设函数 ,
, ,(其中
,(其中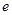 为自然底数);
为自然底数);
(Ⅰ)求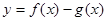 (
( )的最小值;
)的最小值;
(Ⅱ)探究是否存在一次函数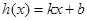 使得
使得 且
且 对一切
对一切 恒成立;若存在,求出一次函数的表达式,若不存在,说明理由;
恒成立;若存在,求出一次函数的表达式,若不存在,说明理由;
(Ⅲ)数列 中,
中,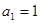 ,
,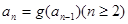 ,求证:
,求证: 。
。
(满分15分)动圆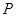 过定点
过定点 且与直线
且与直线 相切,圆心
相切,圆心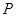 的轨迹为曲线
的轨迹为曲线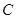 ,过
,过 作曲线
作曲线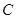 两条互相垂直的弦
两条互相垂直的弦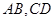 ,设
,设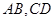 的中点分别为
的中点分别为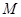 、
、 .
.
(1)求曲线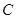 的方程;
的方程;
(2)求证:直线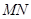 必过定点.
必过定点.
某种鲜花进价每束 元,售价每束
元,售价每束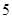 元,若卖不出,则以每束
元,若卖不出,则以每束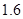 元的价格处理掉。某节日需求量
元的价格处理掉。某节日需求量 (单位:束)的分布列为
(单位:束)的分布列为
 |
200 |
300 |
400 |
500 |
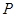 |
 |
 |
 |
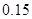 |
(Ⅰ)若进鲜花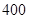 束,求利润
束,求利润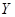 的均值。
的均值。
(Ⅱ)试问:进多少束花可使利润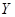 的均值最大?
的均值最大?