如图,已知半径为 的⊙
的⊙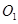 与
与 轴交于
轴交于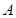 、
、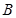 两点,
两点, 为⊙
为⊙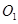 的切线,切点为
的切线,切点为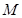 ,且
,且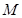 在第一象限,圆心
在第一象限,圆心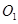 的坐标为
的坐标为 ,二次函数
,二次函数 的图象经过
的图象经过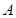 、
、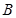 两点.
两点.
(1)求二次函数的解析式;
(2)求切线 的函数解析式;
的函数解析式;
(3)线段 上是否存在一点
上是否存在一点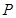 ,使得以
,使得以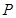 、
、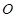 、
、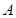 为顶点的三角形与
为顶点的三角形与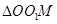 相似.若存在,请求出所有符合条件的点
相似.若存在,请求出所有符合条件的点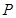 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
若数列 满足
满足 ,其中
,其中 为常数,则称数列
为常数,则称数列 为等方差数列,已知等方差数列
为等方差数列,已知等方差数列 满足
满足 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和;
项和;
(3)记 ,则当实数
,则当实数 大于4时,不等式
大于4时,不等式 能否对于一切的
能否对于一切的 恒成立?请说明理由。
恒成立?请说明理由。
甲、乙两物体分别从相距70m处的两处同时相向运动,甲第一分钟走2m,以后每分钟比前一分钟多走1m,乙每分钟走5m。
(1)甲、乙开始运动后几分钟相遇?
(2)如果甲、乙到达对方起点后立即折返,甲继续每分钟比前一分钟多走1m,乙继续每分钟走5m,那么开始运动几分钟后第二次相遇?
已知A、B、C三点的坐标分别是A(3,0),B(0,3),C ,其中
,其中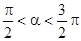 ,
,
(1)若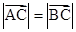 ,求角
,求角 的值;
的值;
(2)若 ,求
,求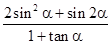 的值。
的值。
等差数列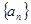 中,前三项分别为
中,前三项分别为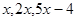 ,前
,前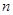 项和为
项和为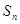 ,且
,且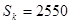 。
。
(1)、求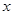 和
和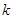 的值;(2)、求T=
的值;(2)、求T=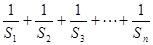
已知 中,
中, 求:(1)边b的长;(2)求
求:(1)边b的长;(2)求 的面积。
的面积。