一质量为m=2kg的木块放在水平地面上,如图所示。在力F作用下从静止开始匀加速运动,经时间t撤去力F,木块作匀减速运动直到停止。从木块开始运动起计时,下表给出了某些时刻木块的瞬时速度。
| 时刻(s) |
1.0 |
2.0 |
3.0 |
5.0 |
7.0 |
9.0 |
11.0 |
| 速度(m/s) |
4.0 |
8.0 |
12.0 |
14.0 |
10.0 |
6.0 |
2.0. |
根据表中的数据通过分析、计算下列问题: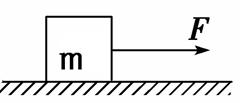
(1)木块与地面间的动摩擦因数μ
(2)力F大小
(3)木块通过的总路程是多少?
有一台发电机通过升压和降压变压器给用户供电,已知发电机的输出功率是300kW,端电压为800V,升压变压器原、副线圈的匝数比为n1∶n2=1:15,两变压器之间输电导线的总电阻r=1.0 ,降压变压器输出电压U4=220V,求:
,降压变压器输出电压U4=220V,求:
(1)升压变压器的输出电压.
(2)输送线路损失的功率.
(3)输送线路损失的电压.
(4)降压变压器的原、副线圈的匝数比.
半径R="1" m的四分之一圆弧轨道下端与一水平轨道连接,水平轨道离地面高度h="0.8" m,如图所示,有一质量m="1.0" kg的小滑块自圆轨道最高点A由静止开始滑下,经过水平轨道末端B,滑块最终落在地面上C点.经测量得x="1.6" m(g取10 m/s2)试求: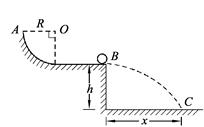
(1) 不计空气阻力,滑块落在地面上时速度vc多大?方向如何?
(2) 滑块在AB轨道上滑行时克服摩擦力做功多少?
如图所示,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经3.0 s落到斜坡上的A点。已知O点是斜坡的起点。斜坡与水平面的夹角θ=37°,运动员的质量m=50 kg.不计空气阻力。(取sin37°=0.60,cos37°=0.80;g取10m/s2)求:
(1)A点与O点的距离L;
(2)运动员离开O点时的速度大小。
能源短缺和环境恶化已经成为关系到人类社会能否持续发展的大问题。为缓解能源紧张压力、减少环境污染,汽车制造商纷纷推出小排量经济实用型轿车。某公司研制开发了某型号小汽车发动机的额定功率为24 kW,汽车连同驾乘人员总质量为m=2 t,在水平路面上行驶时受到的阻力是800 N,求:
(1)汽车在额定功率下匀速行驶的速度;
(2)汽车在额定功率下行驶,速度为20 m/s时的加速度。
如图所示,质量m=2kg的物体处于水平地面上,在推力F作用下由静止开始向右运动了一段距离s=2m。已知图中θ=37°,力F的大小为10N,物体与地面间的滑动摩擦因数μ=0.2,g取10 m/s2。求:
(1)推力F1对物体所做的功;
(2)摩擦力f对物体所做的功;
(3)外力对物体所做的总功。