如图所示,两足够长的平行光滑的金属导轨MN、PQ相距为L=1m,导轨平面与水平面夹角α=30°,导轨电阻不计。磁感应强度为B1=2T的匀强磁场垂直导轨平面向上,长为L=1m的金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m1=2kg、电阻为R1=1Ω。两金属导轨的上端连接右侧电路,电路中通过导线接一对水平放置的平行金属板,两板间的距离和板长均为d=0.5m,定值电阻为R2=3Ω,现闭合开关S并将金属棒由静止释放,取g=10m/s2,求: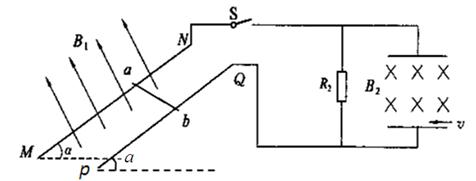
(1)金属棒下滑的最大速度为多大?
(2)当金属棒下滑达到稳定状态时,整个电路消耗的电功率P为多少?
(3)当金属棒稳定下滑时,在水平放置的平行金属间加一垂直于纸面向里的匀强磁场B2=3T,在下板的右端且非常靠近下板的位置处有一质量为m2=3×10-4kg、所带电荷量为q=-1×10-4C的液滴以初速度v水平向左射入两板间,该液滴可视为质点。要使带电粒子能从金属板间射出,初速度v应满足什么条件?
如图所示,某位马拉松选手从A点静止出发,沿曲线ABCDE轨迹的箭头方向运动,AB、ABC、ABCD、ABCDE四段曲线轨迹运动所用的时间分别是:10 s、20s、40s、60s。
(1)如果要研究此位选手的速度变化特征,能否把运动员看成质点?
(2)如果选手在AB段的前4s做匀加速直线运动,之后做匀速直线运动,求加速度为多大?
(3)求选手在ABCD段的平均速度。
如图所示,两块相同的金属板M和N正对并水平放置,它们的正中央分别有小孔O和O′,两板距离为2L,两板间存在竖直向上的匀强电场;AB是一根长为3L的轻质绝缘竖直细杆,杆上等间距地固定着四个(1、2、3、4)完全相同的带电荷小球,每个小球带电量为q、质量为m、相邻小球间的距离为L,第1个小球置于O孔处.将AB杆由静止释放,观察发现,从第2个小球刚进入电场到第3个小球刚要离开电场,AB杆一直做匀速直线运动,整个运动过程中AB杆始终保持竖直,重力加速度为g.求:
(1)两板间的电场强度E;
(2)第4个小球刚离开电场时AB杆的速度;
(3)从第2个小球刚进入电场开始计时,到第4个小球刚离开电场所用的时间。
如图所示的电路中,电源电动势E = 6.0V,内阻r = 0.6Ω,电阻R2 = 0.5Ω,当开关S断开时,理想电流表的示数为1.5A,理想电压表的示数为3.0V,试求: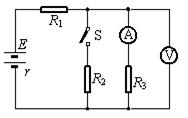
(1)电阻R3和R1的阻值;
(2)当S闭合后,电压表的示数以及R2上消耗的电功率。
一束电子流在经U =5000V的加速电压加速后,在距两极板等距处垂直进入平行板间的匀强电场,如图所示.若两板间距d ="1.0" cm,板长l ="5.0" cm,那么,要使电子能 从平行板间飞出,两个极板上最多能加多大电压? 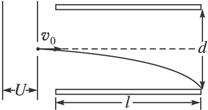
“10米折返跑”的成绩反应了人体的灵敏素质.如图所示,测定时,在平直跑道上,受试者以站立式起跑姿势站在起点终点线前,当听到“跑”的口令后,全力跑向正前方10米处的折返线,测试员同时开始计时.受试者到达折返线处时,用手触摸折返线处的物体(如木箱),再转身跑向起点终点线,当胸部到达起点终点线时,测试员停表,所用时间即为“10米折返跑”的成绩.设受试者起跑的加速度为4m/s2,运动过程中的最大速度为4 m/s,快到达折返线处时需减速到零,减速的加速度为8m/s2,返回时达到最大速度后不需减速,保持最大速度冲线.(受试者在加速和减速过程都可以看作匀变速直线运动)求: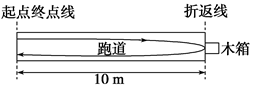
(1)该受试者由起点终点线向折返线运动的时间为多少秒?
(2)该受试者“10米折返跑”的成绩为多少秒?