设函数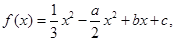 其中
其中 ,曲线
,曲线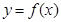 在点
在点 处的切线方程为
处的切线方程为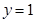 .
.
(I)确定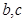 的值;
的值;
(II)设曲线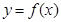 在点
在点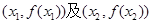 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当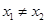 时,
时,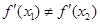 ;
;
(III)若过点(0,2)可作曲线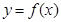 的三条不同切线,求
的三条不同切线,求 的取值范围.
的取值范围.
已知等差数列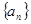 前
前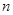 项和为
项和为 ,且
,且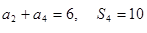
(Ⅰ)求数列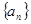 的通项公式;
的通项公式;
(Ⅱ)令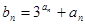 (
(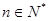 )求数列
)求数列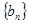 前
前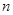 项和为
项和为
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等。
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
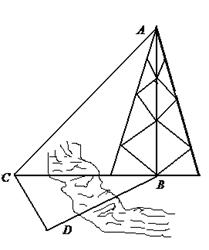
如图,测量河对岸的塔高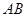 时,可以选与塔底
时,可以选与塔底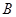 在同一水平面内的两个测点
在同一水平面内的两个测点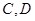 .现测得
.现测得
 ,并在点
,并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 , 求塔高
, 求塔高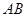 (精确到
(精确到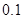 ,
,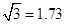 )
)
已知数列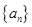 的前
的前 项和为
项和为 ,且
,且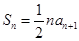 (
( N*),其中
N*),其中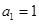 .
.
(Ⅰ) 求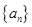 的通项公式;
的通项公式;
(Ⅱ) 设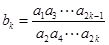 (
( N*).
N*).
①证明:  ;
;
② 求证: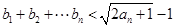 .
.
已知各项都不为零的数列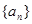 的前n项和为
的前n项和为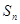 ,
, ,向量
,向量 ,其中
,其中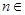 N*,且
N*,且 ∥
∥ .
.
(Ⅰ)求数列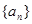 的通项公式及
的通项公式及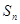 ;
;
(Ⅱ)若数列 的前n项和为
的前n项和为 ,且
,且 (其中
(其中 是首项
是首项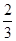 ,第四项为
,第四项为 的等比数列的公比),求证:
的等比数列的公比),求证: .
.