某数学兴趣小组开展了一次课外活动,过程如下:如图,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合。三角板的一边交AB于点P,另一边交BC的延长线于点Q.
(1)求证:DP=DQ;
(2)如图,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;
(3)如图,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△DEP的面积。
如图,三角形ABC是由三角形A1B1C1平移后得到的,三角形ABC中任意一点P(x,y)经平移后对应点为P1(x-3,y-5),求A1、B1、C1的坐标.
如图,梯形A′B′C′D′可以由梯形ABCD经过怎样的平移得到?对应点的坐标有什么变化?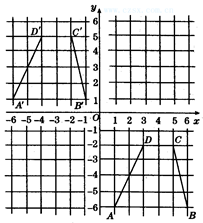
如图,菱形ABCD,四个顶点分别是A(-2,1),B(1,-3),C(4,-1),D(1,1).将菱形沿x轴负方向平移3个单位长度,各个顶点的坐标变为多少?将它沿y轴正方向平移4个单位长度呢?分别画出平移后的图形.
在平面直角坐标系中,△ABC的边AB在x轴上,且AB=3,顶点A的坐标为(-5,0),顶点C的坐标为(2,5).
(1).画出所有符合条件的△ABC,并直接写出点B的坐标.
(2).求△ABC的面积.
如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.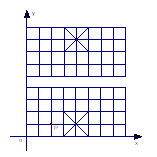
⑴写出下一步“马”可能到达的点的坐标 ;
⑵顺次连接⑴中的所有点,得到的图形是 图形(填“中心对称”、“旋转对称”、“轴对称”);
⑶指出⑴中关于点P成中心对称的点 .