在天津市科技馆中,有一个模拟万有引力的装置。在如上图所示的类似锥形漏斗固定的容器中,有两个小球在该容器表面上绕漏斗中心轴做水平圆周运动,其运行能形象地模拟了太阳系中星球围绕太阳的运行。图2为示意图,图3为其模拟的太阳系运行图。图1中离中心轴的距离相当于行星离太阳的距离。则:
(1)在图3中,设行星A1和B1离太阳距离分别为r1和r2,求A1和B1运行速度大小之比。
(2)在图2中,若质量为m的A球速度大小为v,在距离中心轴为x1的轨道面上旋转,由于受到微小的摩擦阻力,A球绕轴旋转同时缓慢落向漏斗中心。当其运动到距离中心轴为x2的轨道面时,两轨道面之间的高度差为H。请估算此过程中A球克服摩擦阻力所做的功。
如图所示,一束电子(电荷量为e)以速度v垂直射入磁感应强度为B、宽度为d的匀强磁场中,电子穿出磁场时速度方向与入射方向的夹角为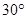 ,电子的重力忽略不计,求:
,电子的重力忽略不计,求:
(1)电子的质量m ;
(2)穿过磁场的时间t 。
如图所示,电阻 ,小灯泡
,小灯泡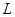 上标有“3V,1.5W”,电源内阻
上标有“3V,1.5W”,电源内阻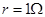 ,滑动变阻器的最大阻值为
,滑动变阻器的最大阻值为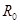 (大小未知),当触头
(大小未知),当触头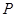 滑动到最上端
滑动到最上端 时,电流表的读数为l A,小灯泡
时,电流表的读数为l A,小灯泡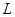 恰好正常发光,求:
恰好正常发光,求:
(1)滑动变阻器的最大阻值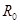 ;
;
(2)当触头 滑动到最下端
滑动到最下端 时,求电源的总功率及输出功率。
时,求电源的总功率及输出功率。
如图所示的滑轮,它可以绕垂直于纸面的光滑固定水平轴O转动,轮上绕有轻质柔软细线,线的一端系一质量为3m的重物,另一端系一质量为m,电阻为r的金属杆.在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电阻,其余电阻不计,磁感应强度为Bo的匀 强磁场与导
强磁场与导 轨平面垂直,开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降.运动过程中金属杆始终与导轨垂直且接触良好,忽略所有摩
轨平面垂直,开始时金属杆置于导轨下端QF处,将重物由静止释放,当重物下降h时恰好达到稳定速度而匀速下降.运动过程中金属杆始终与导轨垂直且接触良好,忽略所有摩 擦,求:
擦,求:
(1)重物匀速下降的速度v;
(2)重物从释放到下降h对的过程中,电阻R中产 生的焦耳热QR;
生的焦耳热QR;
(3)若将重物下降h时的时刻记作t=0,从此时刻起,磁感应强度逐渐减小,若此后金属杆中恰好不产生感应电流,则磁感应强度B怎样随时间t变化(写出B与t的关系式).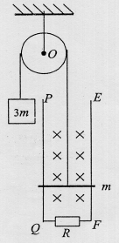
如图,一匀强磁场磁感应强度为B,方向垂直纸面向里,其边界是半径为R的圆.MN为圆的一直径.在M点有一粒子源可以在圆平面内向不同方向发射质量m、电量-q速度为v的粒子,粒子重力不计,其运动轨迹半径大于R.
( 1)求粒子在圆形磁场中运动的最长时间(答案中可包含某角度,需注明该角度的正弦或余弦值);
1)求粒子在圆形磁场中运动的最长时间(答案中可包含某角度,需注明该角度的正弦或余弦值);
(2)试证明:若粒子沿半径方向入射,则粒子一定沿半径方向射出磁场.
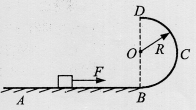
如图所示,水平轨道AB与位于竖直面内半径为R的半圆形光滑轨道BCD相连,半圆形轨道的直径BD与AB垂直,水平轨道上有一质量m=1.0kg可看作质点的小滑块,滑块与水平 轨道间的动摩擦因数μ=0.5.现使滑块从水平轨道上某点静止起出发,在水平向右的恒力F作用下运动,到达水平轨道的末端B点时撤去外力F,小滑块继续沿半圆形轨道运动;恰好能通过轨道最高点D,滑块脱离半圆形轨道后又刚好落到其出发点,g取10m/s2.
(1)当R=0.90m时,求其出发点到B点之间的距离x及滑块经过B点进入圆形轨道时对轨道的压力大小;
(2)小明同学认为:若半圆形光滑轨道BCD的半径R取不同数值,仍要使物体恰好能通过D点飞离圆轨道并刚好落回其对应的出发点,恒定外力F的大小也应随之改变。你是否同意他的观点,若同意 ,求出F与R的关系式;若不同意,请通过计算说明。
,求出F与R的关系式;若不同意,请通过计算说明。