人类受小鸟在空中飞翔的启发而发明了飞机,小鸟在空中滑翔时获得向上的举力可表示为F=kSv2,式中S为翅膀的面积,v为小鸟飞行的速度,k为比例系数,一小鸟质量为120g,翅膀面积为S1,其水平匀速滑翔的最小速度为12m/s。假定飞机在跑道上滑行时获得向上的举力与小鸟滑翔时获得的举力有同样的规律。现有一架质量为3200kg的飞机,其机翼面积为600S1,若它在跑道上由静止开始匀加速滑行,加速度a=5m/s2,求此飞机起飞前在跑道上滑行的距离。
如图9所示,LC电路中C是带有电荷的平行板电容器,两极板水平放置.开关S断开时,极板间灰尘恰好静止.当开关S闭合时,灰尘在电容器内运动,若C=0.4 μF,
L=1 mH,求: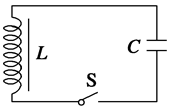
图9
(1)从S闭合开始计时,经2π×10-5 s时,电容器内灰尘的加速度大小为多少?
(2)当灰尘的加速度多大时,线圈中电流最大?
实验证明让一束太阳光入射到平静的水面上,如果入射角合适,其反射光线和折射光线是互相垂直的,且偏振方向也是互相垂直的偏振光。已知水的折射率为1.33,求这一入射角为多少?
单色细光束射到折射率n= 的透明球表面,光束在过球心的平面内,入射角i=45°,经折射进入球内后又经内表面反射一次,再经球表面折射后射出的光线,如图13-7-18所示(图上已画出入射光线和出射光线).
的透明球表面,光束在过球心的平面内,入射角i=45°,经折射进入球内后又经内表面反射一次,再经球表面折射后射出的光线,如图13-7-18所示(图上已画出入射光线和出射光线).
图13-7-18
(1)在图上大致画出光线在球内的路径和方向;
(2)求入射光线与出射光线之间的夹角α;
(3)如果入射的是一束白光,透明球的色散情况与玻璃相仿,问哪种颜色光的α角最大,哪种颜色光的α角最小?
为了减少光在透镜表面由于反射带来的损失,可在透镜表面涂上一层增透膜,一般用折射率为1.38的氟化镁,为了使波长为5.52×10-7 m的绿光在垂直表面入射时使反射光干涉相消,求所涂的这种增透膜的厚度.
一种红宝石激光器发射的激光是不连续的一道道闪光,每道闪光称为一个光脉冲,若这种激光器光脉冲的持续时间为1.0×10-11 s,波长为694.3 nm,发射功率为1.0×1010 W.
(1)每列光脉冲的长度是多少?
(2)用红宝石激光照射皮肤色斑,每1 cm2吸收能量达到60 J以后,色斑便逐渐消失,一颗色斑的面积是50 mm2,则它需要吸收多少个红宝石激光脉冲才能逐渐消失?