已知,如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(21,0),C(0,6),动点D在线段AO上从点A以每秒2个单位向点O运动,动点P在线段BC上从点C以每秒1个单位向点B运动.若点D点P同时运动,当其中一个动点到达线段另一个端点时,另一个动点也随之停止.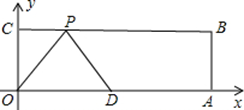
(1)求点B的坐标;
(2)设点P运动了t秒,用含t的代数式表示△ODP的面积S;
(3)当P点运动某一点时,是否存在使△ODP为直角三角形,若存在,求出点P的坐标,若不存在说明理由.
下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数。”
解:如图,∵AD⊥BC,AD= BC=BD=CD,
BC=BD=CD,
∴∠BAD=∠B=∠C=∠CAD=45°,
∴∠BAC=90°
你认为小明的解答正确吗?若不正确,请你将它补充完整。
阅读下面短文:如图1,△ABC是直角三角形,∠C=90°,现将△ABC补成长方形,使△ABC的两个顶点为长方形一边的两个端点,第三个顶点落在长方形这一边的对边上,那么符合要求的长方形可以画出两个:长方形ACBD和长方形AEFB(如图2)。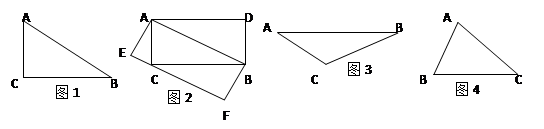
解答问题:
(1)设图2中长方形ACBD和长方形AEFB的面积分别为S1,S2,则S1S2(填“>”、“=”或“<”)
(2)如图3,△ABC是钝角三角形,按短文中的要求把它补成长方形,那么符合要求的长方形可以画出个,利用图3把它画出来。
(3)如图4,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成长方形,那么符合要求的长方形可以画出个,利用图4把它画出来。
(4)在(3)中所画出的长方形中,哪一个的周长最小?为什么?
等腰三角形的一腰上的高为10cm,这条高与底边的夹角为45°,求它的面积。
给你一副三角板,你能用它拼出几个度数不同的角?请把它们都写出来。
求直角三角形两锐角平分线所夹的锐角的度数。