某公司承担了每天至少搬运280吨水泥的任务,已知该公司有6辆A型卡车和8辆B型卡车.又已知A型卡车每天每辆的运载量为30吨,成本费为0.9千元;B型卡车每天每辆的运载量为40吨,成本费为1千元.
(1)如果你是公司的经理,为使公司所花的成本费最小,每天应派出A型卡车、B型卡车各多少辆?
(2)在(1)的所求区域内,求目标函数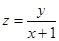 的最大值和最小值.
的最大值和最小值.
用平行于棱锥底面的平面去截棱锥,则截面与底面之间的部分叫棱台.如图,在四棱台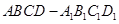 中,下底
中,下底 是边长为
是边长为 的正方形,上底
的正方形,上底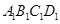 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱 ⊥平面
⊥平面 ,
, .
.
(Ⅰ)求证: 平面
平面 ;
;
(II)求平面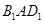 与平面
与平面 夹角的余弦值.
夹角的余弦值.
已知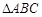 中,角
中,角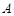 、
、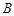 、
、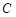 的对边分别为
的对边分别为 、
、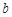 、
、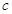 ,角
,角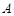 不是最大角,
不是最大角,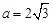 ,外接圆的圆心为
,外接圆的圆心为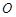 ,半径为
,半径为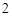 .
.
(Ⅰ)求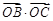 的值;
的值;
(Ⅱ)若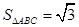 ,求
,求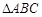 的周长
的周长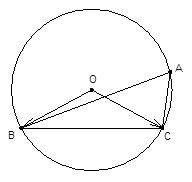
已知数列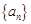 满足
满足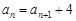 ,
,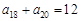 ,等比数列
,等比数列 的首项为2,公比为
的首项为2,公比为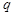 .
.
(Ⅰ)若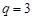 ,问
,问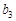 等于数列
等于数列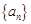 中的第几项?
中的第几项?
(Ⅱ)数列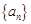 和
和 的前
的前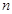 项和分别记为
项和分别记为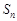 和
和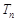 ,
,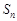 的最大值为
的最大值为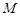 ,当
,当 时,试比较
时,试比较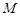 与
与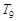 的大小
的大小
对于数列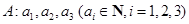 ,定义“
,定义“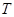 变换”:
变换”: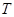 将数列
将数列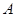 变换成数列
变换成数列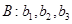 ,其中
,其中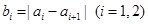 ,且
,且 .这种“
.这种“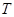 变换”记作
变换”记作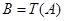 .继续对数列
.继续对数列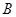 进行“
进行“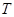 变换”,得到数列
变换”,得到数列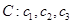 ,依此类推,当得到的数列各项均为
,依此类推,当得到的数列各项均为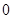 时变换结束.
时变换结束.
(Ⅰ)试问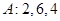 经过不断的“
经过不断的“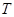 变换”能否结束?若能,请依次写出经过“
变换”能否结束?若能,请依次写出经过“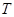 变换”得到的各数列;若不能,说明理由;
变换”得到的各数列;若不能,说明理由;
(Ⅱ)设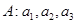 ,
,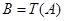 .若
.若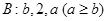 ,且
,且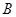 的各项之和为
的各项之和为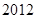 .
.
(ⅰ)求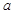 ,
,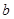 ;
;
(ⅱ)若数列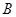 再经过
再经过 次“
次“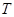 变换”得到的数列各项之和最小,求
变换”得到的数列各项之和最小,求 的最小值,并说明理由.
的最小值,并说明理由.
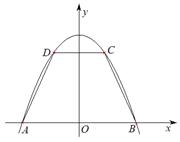
如图,抛物线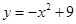 与
与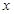 轴交于两点
轴交于两点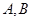 ,点
,点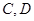 在抛物线上(点
在抛物线上(点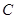 在第一象限),
在第一象限),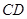 ∥
∥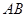 .记
.记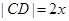 ,梯形
,梯形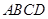 面积为
面积为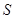 .
.
(Ⅰ)求面积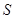 以
以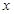 为自变量的函数式;
为自变量的函数式;
(Ⅱ)若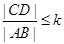 ,其中
,其中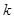 为常数,且
为常数,且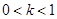 ,求
,求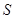 的最大值.
的最大值.