已知点F是抛物线C: 的焦点,S是抛物线C在第一象限内的点,且|SF|=
的焦点,S是抛物线C在第一象限内的点,且|SF|= .
.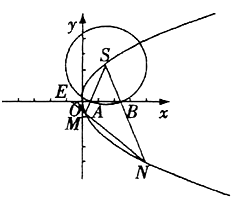
(Ⅰ)求点S的坐标;
(Ⅱ)以S为圆心的动圆与 轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
轴分别交于两点A、B,延长SA、SB分别交抛物线C于M、N两点;
①判断直线MN的斜率是否为定值,并说明理由;
②延长NM交 轴于点E,若|EM|=
轴于点E,若|EM|= |NE|,求cos∠MSN的值.
|NE|,求cos∠MSN的值.
(本小题满分14分)
等差数列{an}不是常数列,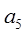 =10,且
=10,且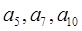 是等比数列{
是等比数列{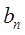 }的第1,3,5项,且
}的第1,3,5项,且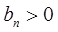 .
.
(1)求数列{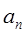 }的第20项,(2)求数列{
}的第20项,(2)求数列{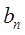 }的通项公式.
}的通项公式.
(本小题满分14分)
已知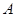 、
、 、
、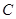 为
为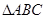 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、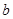 、
、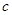 ,若
,若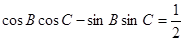 .
.
(1)求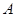 ; (2)若
; (2)若 ,求
,求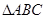 的面积.
的面积.
(本小题满分12分)
已知等差数列 中,
中,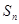 是其前
是其前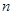 项和,
项和,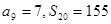 ,求:
,求: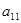 及
及 .
.
若等差数列 的前
的前 项和为
项和为 ,且满足
,且满足 为常数,则称该数列为
为常数,则称该数列为 数列.
数列.
(1)判断 是否为
是否为 数列?并说明理由;
数列?并说明理由;
(2)若首项为 且公差不为零的等差数列
且公差不为零的等差数列 为
为 数列,试求出该数列的通项公式;
数列,试求出该数列的通项公式;
(3)若首项为 ,公差不为零且各项为正数的等差数列
,公差不为零且各项为正数的等差数列 为
为 数列,正整数
数列,正整数 满足
满足 ,求
,求 的最小值
的最小值
已知函数 ,当
,当 时,
时, ;
;
当 时,
时, .
.
(1)求 在
在 内的值域;
内的值域;
(2) 为何值时,
为何值时, 的解集为
的解集为 .
.