随着航天技术的发展,在地球周围有很多人造飞行器,其中有一些已超过其设计寿命且能量耗尽。每到太阳活动期,地球的大气层会变厚,这时有些飞行器在大气阻力的作用下,运行的轨道高度将逐渐降低(在其绕地球运动的每一周过程中,轨道高度变化很小,均可近似视为匀速圆周运动)。为了避免飞行器坠入大气层后对地面设施及人员造成安全威胁,人们设想发射导弹将其在运行轨道上击碎。具体设想是:在导弹的弹头脱离推进装置后,经过一段无动力飞行,从飞行器后下方逐渐接近目标,在进入有效命中距离后引爆弹头并将该飞行器击碎。对于这一过程中的飞行器及弹头,下列说法中正确的是( )
| A.飞行器轨道高度降低后,它做圆周运动的速率变大 |
| B.飞行器轨道高度降低后,它做圆周运动的周期变大 |
| C.弹头在脱离推进装置之前,始终处于失重状态 |
| D.弹头引爆前瞬间,弹头的加速度一定小于此时飞行器的加速度 |
如图所示,一电量为q的带电粒子在竖直向上的匀强电场E和垂直纸面向里的匀强磁场B正交的空间区域做竖直平面内的匀速圆周运动,重力加速度为g,则下列说法正确的是( )
| A.粒子带负电 |
| B.粒子沿逆时针方向做匀速圆周运动 |
| C.粒子的质量为Eq/g |
| D.粒子从圆轨道的最高点运动到最低点的时间为πE/gB |
1932年,美国的物理学家劳伦斯设计出了回旋加速器。回旋加速器的工作原理如图所示,置于高真空中的两D形金属盒半径为R,两盒间的狭缝很小,带电粒子穿过的时间可以忽略不计。磁感应强度为B的匀强磁场与盒面垂直。A处粒子源产生的质量为m、电荷量为+q粒子在加速器中被加速,其加速电压恒为U。带电粒子在加速过程中不考虑相对论效应和重力的作用。则()
| A.带电粒子在加速器中第1次和第2次做曲线运动的时间分别为t1和t2,则t1:t2=1:2 |
B.带电粒子第1次和第2次经过两D形盒间狭缝后轨道半径之比r1:r2= :2 :2 |
C.两D形盒狭缝间的交变电场的周期T=2 m/qB m/qB |
| D.带电粒子离开回旋加速器时获得的动能为B2q2R2/2m |
在如图所示的电路中,闭合开关S,当滑动变阻器的滑动触头P向下滑动时,四个理想电表的示数都发生变化,电表的示数分别用I、U1、U2和U3表示,电表示数变化量的大小分别用ΔI、ΔU1、ΔU2和ΔU3表示.下列比值正确的是()
| A.U1/I不变,ΔU1/ΔI不变 | B.U2/I变大,ΔU2/ΔI变大 |
| C.U2/I变大,ΔU2/ΔI不变 | D.U3/I变大,ΔU3/ΔI不变 |
如图所示,表示一交变电流随时间变化的图象,此交流电的有效值是()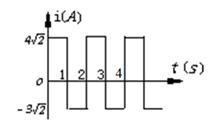
A.5 A A |
B.5A |
C.3.5 A A |
D.3.5A |
如图所示,T为理想变压器,副线圈回路中的输电线ab和cd的电阻不可忽略,其余输电线电阻可不计,则当开关S闭合时()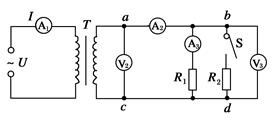
| A.交流电压表V2和V3的示数一定都变小 |
| B.交流电压表V3的示数变小 |
| C.交流电流表A1、A2和A3的示数一定变大 |
| D.只有A1的示数变大 |