数列 前
前 项和
项和 ,数列
,数列 满足
满足 (
( ),
),
(1)求数列 的通项公式;
的通项公式;
(2)求证:当 时,数列
时,数列 为等比数列;
为等比数列;
(3)在(2)的条件下,设数列 的前
的前 项和为
项和为 ,若数列
,若数列 中只有
中只有 最小,求
最小,求 的取值范围.
的取值范围.
已知椭圆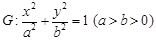 的离心率为
的离心率为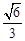 ,右焦点为
,右焦点为 ,过原点
,过原点 的直线
的直线 交椭圆于
交椭圆于 两点,线段
两点,线段 的垂直平分线交椭圆
的垂直平分线交椭圆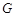 于点
于点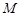 .
.
(Ⅰ)求椭圆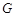 的方程;
的方程;
(Ⅱ)求证: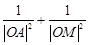 为定值,并求
为定值,并求 面积的最小值.
面积的最小值.
甲乙两个同学进行定点投篮游戏,已知他们每一次投篮投中的概率均为 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.
(1)求甲同学至少有4次投中的概率;
(2)求乙同学投篮次数 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)如图,四边形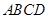 是正方形,△
是正方形,△ 与△
与△ 均是以
均是以 为直角顶点的等腰直角三角形,点
为直角顶点的等腰直角三角形,点 是
是 的中点,点
的中点,点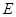 是边
是边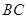 上的任意一点.
上的任意一点.
(1)求证: ;
;
(2)求二面角 的平面角的正弦值.
的平面角的正弦值.
已知向量 ,
, ,函数
,函数
(1)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)在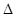
 中,
中, 分别是角
分别是角 的对边,且
的对边,且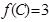 ,
, ,
,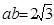 ,且
,且 ,求
,求 的值.
的值.
选修4—5: 不等式选讲.
(Ⅰ)设函数 .证明:
.证明: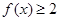 ;
;
(Ⅱ)若实数 满足
满足 ,求证:
,求证: