如图（1），在平面直角坐标系中，AB⊥x轴于B，AC⊥y轴于C，点C（0，m），A（n，m），且（m-4）2+n2-8n＝-16，过C点作∠ECF分别交线段AB、OB于E、F两点.
（1）求A点的坐标；
（2）若OF+BE＝AB，求证：CF＝CE
（3）如图（2），若∠ECF＝45°，给出两个结论：OF+AE-EF的值不变；OF+AE+EF的值不变，其中有且只有一个结论正确，请你判断出正确的结论，并加以证明和求出其值.
（本小题满分8分）
（1）解不等式组：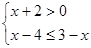
；
（2）解方程：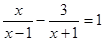
.
（本小题满分8分）
（1）
；
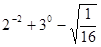（2）化简：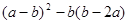
.
如图，若二次函数
的图像过点A（－1，0），C（0，
），与x轴的另一交点为B，D为顶点．
（1）求m、n的值及B、D两点的坐标；
（2）若二次函数的图像的对称轴与x轴的交点为P，在线段BC上找一点Q，使得以点B、P、Q为顶点的三角形与△ABC相似，请求出所有符合条件的点Q坐标；
（3）将△ABC沿x轴向右平移t个单位长度（0<t<6），设平移后的△ABC与△PBD重叠的面积为S，请直接写出S 与t的函数关系式．
已知，直线AP是过正方形ABCD顶点A的任一条直线（不过B、C、D三点），点B关于直线AP的对称点为E，连结AE、BE、DE，直线DE交直线AP于点F．
（1）如图1，直线AP与边BC相交．
①若∠PAB=20°，则∠ADF=°，∠BEF=°；
②请用等式表示线段AB、DF、EF之间的数量关系，并说明理由；
（2）如图2，直线AP在正方形ABCD的外部，且
，
，求线段AF的长．
如图，已知AB是⊙O的直径，C为⊙O外一点，连结CO并延长交⊙O于点D、E，连结BD并延长交AC于点F，连结AD，∠DAF=∠B．
（1）求证：CA是⊙O的切线；
（2）若AB=6，CA=4，求CD的长；
（3）在（2）的条件下，求tan∠CDF的值．