在“探究加速度与力、质量的关系”实验中,采用下图所示的实验装置。
(1)本实验采用的实验方法是
A.控制变量法 B.理想实验法
C.等效替代法 D.实验推理法
(2)下列说法中正确的是
A.在探究加速度与质量的关系时,应该改变拉力的大小
B.在探究加速度与外力的关系时,应该改变小车的质量
C.在探究加速度a与质量m的关系时,为了直观判断二者的关系,应作出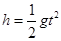 图象
图象
D.当小车的质量远小于砝码盘和砝码的总质量时,才能近似认为细线对小车的拉力大小等于砝码盘和砝码的总重力大小
E.平衡摩擦力时应将砝码盘及盘内砝码通过定滑轮系在小车上
某同学将铜片和锌片插入水果中制成一个“水果电池”,该同学利用下列所给器材测量水果电池的电动势E和内阻r。
A.电流表G1(内阻Rg=l5Ω,满偏电流Ig="2mA)"
B.电流表G2(量程20mA,内阻约2Ω)
C.滑动变阻器R1(0-1000Ω)
D.电阻箱R2(0~9999.9Ω)
E.待测水果电池(电动势E约4V,内阻r约200Ω)
F.开关S,导线若干
(1)实验中用电流表G1改装成量程0~4V的电压表,需(选填“串联”或“并联”)一个阻值为Ω的电阻;
(2)用电流表G2和改装成的电压表测量水果电池的电动势和内阻,为尽量减小实验的误差,请在虚线方框中画出实验电路图;
(3)该同学实验中记录的6组对应的数据如下表,试根据表中数据在下图中描点画出U-I图线;由图线可得,水果电池的电动势E=V,内电阻r=Ω;(结果保留三位有效数字)

(4)实验测得的水果电池的电动势和内阻与真实值相比,E测E真,r测r真(选填“>”、“<”或“=”)。
在“描绘小灯泡的伏安特性曲线”实验中,要测量一个标有“3V 1.5W”的灯泡两端的电压和通过它的电流,现有如下器材:
A.直流电源3V(内阻可不计)
B.直流电表0~3A(内阻约0.1Ω)
C.直流电表0~600mA(内阻约0.5Ω)
D.直流电压表0~3V(内阻约3kΩ)
E.直流电压表0~15V(内阻约200kΩ)
F.滑线变阻器(10Ω,1A)
G.滑线变阻器(1kΩ,300mA)
(1)除开关、导线外,为完成实验,需要从上述器材中选用(用字母)。
(2)某同学用导线a、b、c、d、e、f、g和h连接的电路如图所示,电路中所有元器件都是完好的,且电压表和电流表已调零。闭合开关后发现电压表的示数为2V,电流表的示数为零,小灯泡不亮,则可判断断路的电线是;若电压表示数为零,电流表的示数为0.3A,小灯泡亮,则断路的导线是;若反复调节滑动变阻器,小灯泡亮度发生变化,但电压表、电流表示数不能调为零,则断路的导线是。
(3)下表中的各组数据是该同学在实验中测得的,某位同学根据表格中的数据作出了该灯泡的伏安特性曲线。
若将该灯泡与一个10Ω的定值电阻串联,直接接在题中电源两端,则可以估算出该灯泡的实际功率为W。(结果保留两位有效数字)
在“探究力合成的方法”实验后,某同学认为在该实验中可用弹簧秤取代橡皮条操作更方便,如图所示,三弹簧秤只拉一次即可进行实验验证,任意两拉力的合力与第三拉力实现二力平衡,O为绳套节点.
(1)该同学认为在此实验中必须注意以下几项,其中正确的是.
| A.三根细绳夹角必须要为特定角度值 |
| B.在使用弹簧秤时要注意使弹簧秤与纸面平行 |
| C.每次实验中都要记下三个弹簧秤的示数和拉力方向 |
| D.每次实验操作中不必保持节点O在纸面上的位置不变 |
(2)若两可动弹簧秤的计数如图,则其合力大小为N(在试卷上直接作图求解).此合力与第三弹簧拉力大稍有不同,你认为产生误差的主要原因是(列出两条即可):,。

如图1所示为“探究小车速度随时间变化的规律”实验的装置图.
(1)图2为某次实验时得到的纸带(部分),纸带上每两个计数点间还有四个实验点未标出.则打B点时小车的速度为m/s.(已知电源频率50Hz,结果保留三位有效数字)
(2)利用实验中的某条纸带,所得数据如下表,请你在坐标纸上作出v—t图象,并根据该图像说明小车运动规律:初速为加速度为直线运动.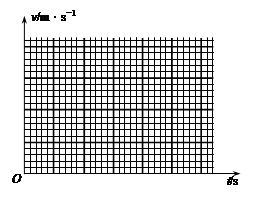
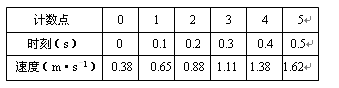
某同学在研究小车运动实验中,获得一条点迹清楚的纸带,已知打点计时器每隔0.02秒打一个计时点,该同学选择ABCDEF六个计数点,对计数点进行测量的结果记录在图中, 单位是cm,
(1)试计算在打下B时小车的瞬时速度vB=______ m/s;CE间的平均速度v=_______m/s ;
(2)计算小车的加速度a=________________m/s2