如图,一个质量为0.6kg 的小球以某一初速度从P点水平抛出,恰好从光滑圆弧ABC的A点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失)。已知圆弧的半径R=0.3m , θ="60" 0,小球到达A点时的速度 v="4" m/s 。(取g ="10" m/s2)求:
(1)小球做平抛运动的初速度v0;
(2)P点与A点的水平距离和竖直高度;
(3)小球到达圆弧最高点C时对轨道的压力。
一架喷气式飞机,对地飞行速度是800m/s,如果它某次喷出气体的质量是200g,相对飞机的速度是600m/s,喷出气体后飞机的质量变为300kg ,那么此次喷气后飞机相对地面的速度为多少
如图中实线是一列简谐横波在t1=0时刻的波形,虚线是这列波在t2=0.5 s时刻的波形,这列波的周期T符合:3T<t2-t1<4T.问: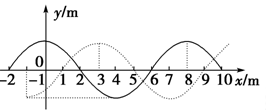
(1)若波速向右,波速多大?
(2)若波速向左,波速多大?
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图所示,介质中质点P、Q分别位于x=2m、x=4m处.从t=0时刻开始计时,当t=15 s时质点Q刚好第4次到达波峰.
(1)求波速;
(2)写出质点P做简谐运动的表达式(不要求推导过程).
汽车的车身是装在弹簧上的,如果这个系统的固有周期是1.5 s,汽车在一条起伏不平的路上行驶,路上各凸起处大约都相隔8 m,汽车以多大速度行驶时,车身上下颠簸得最剧烈?
如图为某种透明材料制成的边长为4cm,横截面为正三角形的三棱镜,将其置于空气中,当一细光束从距离顶点A为1cm的D点垂直于AB面入射时,在AC面上刚好发生全反射,光在真空中的速度c=3×108m/s。求:
①此透明材料的折射率;②光通过三棱镜的时间。