如图所示，左侧为一个半径为R的半球形的碗固定在水平桌面上，碗口水平， O点为球心，碗的内表面及碗口光滑。右侧是一个固定光滑斜面，斜面足够长，倾角θ=30°。一根不可伸长的不计质量的细绳跨在碗口及光滑斜面顶端的光滑定滑轮两端上，线的两端分别系有可视为质点的小球m1和m2，且m1>m2。开始时m1恰在右端碗口水平直径A处， m2在斜面上且距离斜面顶端足够远，此时连接两球的细绳与斜面平行且恰好伸直。当m1由静止释放运动到圆心O的正下方B点时细绳突然断开，不计细绳断开瞬间的能量损失。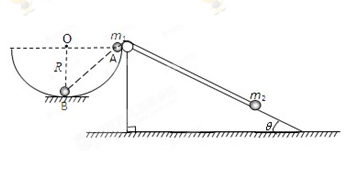
(1)求小球m2沿斜面上升的最大距离s；（2）若已知细绳断开后m1沿碗的内侧上升的最大高度为R/2，求m1/m2。
如图所示，水平放置的A、B两平行金属板的中央各有一小孔O1、O2，板间距离为d，开关S接1。当t=0时，在a、b两端加上如图乙中的①图线所示的电压，同时在c、d两端加上如图丙所示的电压。此时，一质量为m的带负电微粒恰好静止于两孔连线的中点P处 （P、O1、O2在同一竖直线上）。重力加速度为g，空气阻力和金属板的厚度不计。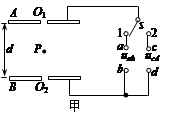
（1）若某时刻突然在a、b两端改加如图乙中的②图线所示的电压，则微粒可达到的最高点距A板的高度为多少？
（2）若要使微粒在两板间运动后，从A板中的O1小孔射出，且射出时的动能尽可能大，求：应在t=0到t=T之间的哪个时刻把开关S从l扳到2位置？ucd的变化周期T至少为多少?
如图，在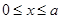
的区域有垂直于纸面向里的匀强磁场，磁感应强度的大小为B，在x>a的区域有垂直于纸面向外的匀强磁场，磁感应强度的大小也为B。质量为m、电荷量为q（q>0）的粒子沿x轴从原点O射入磁场。（粒子重力忽略不计）若粒子以
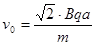的速度射入磁场，求其轨迹与x轴交点的横坐标？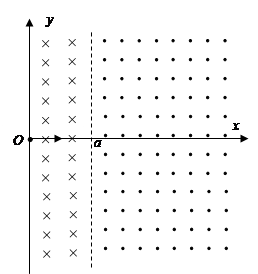
如图所示，QB段为一半径为R的光滑圆弧轨道，AQ段为一长度为R的粗糙水平轨道，二轨道相切于Q点，Q在圆心O的正下方，整个轨道位于同一竖直平面内。 物块P的质量为m（可视为质点），P与AQ间的动摩擦因数μ=0.1；若物块 P以速度v0从A点滑上水平轨道，到C点后又返回A点时恰好静止，重力加速度为g.求：
（1）v0的大小？
（2）P刚越过Q点时对轨道的压力？
桌面上有一轻质弹簧，左端固定在A点，自然状态时其右端B点位于桌面右侧边缘．水平桌面右侧有一竖直放置、半径R＝0.3 m的光滑半圆轨道MNP，桌面与轨道相切于M点．在以MP为直径的右侧和水平半径ON的下方部分有水平向右的匀强电场，场强的大小E＝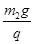
.现用质量m1＝0.4 kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点．用同种材料、质量为m2＝0.2 kg、带＋q的绝缘物块将弹簧缓慢压缩到C点，释放后物块离开桌面由M点沿半圆轨道运动，恰好能通过轨道的最高点P.（取g＝10 m/s2）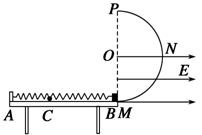
（1）物块m2经过桌面右侧边缘B点时的速度大小；
（2）物块m2在半圆轨道运动时对轨道的最大压力；
（3）释放后物块m2运动过程中克服摩擦力做的功．
在如图所示的电路中，两平行正对金属板A、B水平放置，两板间的距离d=4.0cm。电源电动势E=400V，内电阻r=20
，电阻R1=1980。闭合开关S，待电路稳定后，将一带正电的小球（可视为质点）从B板上的小孔以初速度v0=1.0m/s竖直向上射入两板间，小球恰好能到达A板。若小球所带电荷量q=1.0×10-7C，质量m=2.0×10-4kg，不考虑空气阻力，忽略射入小球对电路的影响，取g=10m/s2。求：
（1）A、B两金属板间的电压的大小U；
（2）滑动变阻器消耗的电功率P滑。