如图，二次函数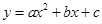
的图象与x轴交于两个不同的点A（﹣2，0）、B（4，0），与y轴交于点C（0，3），连接BC、AC，该二次函数图象的对称轴与x轴相交于点D．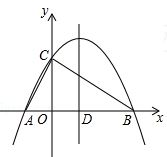
（1）求这个二次函数的解析式、
（2）点D的坐标及直线BC的函数解析式；
（3）点Q在线段BC上，使得以点Q、D、B为顶点的三角形与△ABC相似，求出点Q的坐标；
（4）在（3）的条件下，若存在点Q，请任选一个Q点求出△BDQ外接圆圆心的坐标．
如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
∵EF∥AD，（）
∴∠2=．（两直线平行，同位角相等；）
又∵∠1=∠2，（）
∴∠1=∠3．（）
∴AB∥DG．（）
∴∠BAC+=180°（）
又∵∠BAC=70°，（）
∴∠AGD= ．
解不等式组
，并把解集在数轴上表示出来．
解方程组
．
如图1，已知一次函数y=-
x+6分别与x、y轴交于A、B两点，过点B的直线BC交x轴负半轴与点C，且OC=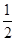
OB.
（1）求直线BC的函数表达式；
（2）如图2，若△ABC中，∠ACB的平分线CF与∠BAE的平分线AF相交于点F，求证：∠AF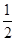C=∠ABC；
（3）在x轴上是否存在点P，使△ABP为等腰三角形？若存在，请直接写出P点的坐标；若不存在，请说明理由.
为表彰在“深圳读书月”活动中表现积极的同学，某班级决定购买文具盒与钢笔作为奖品.已知3个文具盒、2支钢笔共需72元；1个文具盒、2支钢笔共需44元.
（1）每个文具盒、每支钢笔各多少元？
（2）时逢“元旦”，商店举行优惠促销活动，具体办法如下：文具盒九折，钢笔10支以上超出部分八折.设买x1个文具盒需要y1元，买x2支钢笔需要y2元，求y1、y2关于x的函数关系式，并写出自变量的取值范围.