如图，EF∥AD，∠1=∠2，∠BAC=70°．将求∠AGD的过程填写完整．
∵EF∥AD，（ ）
∴∠2=．（两直线平行，同位角相等；）
又∵∠1=∠2，（ ）
∴∠1=∠3．（ ）
∴AB∥DG．（ ）
∴∠BAC+=180°（ ）
又∵∠BAC=70°，（ ）
∴∠AGD= ．
某支股票上周末的收盘价格是10．00元，李先生买了2000股，本周一到周五的这支股票的收盘情况如下表：（“＋”表示股票比前一天上涨，“－”表示股票比前一天下跌）
| 上周末收盘价 |
周一 |
周二 |
周三 |
周四 |
周五 |
| 10．00 |
＋0．28 |
－0．36 |
＋0．38 |
－0．35 |
＋0．25 |
（1）周三这支股票的收盘价是多少元？
（2）本周末的收盘价与上周末收盘价相比是怎样变化的？
（3）李先生在本周五将股票全部卖出，若不考虑其他因素，请分析李先生在本次股票买卖过程中的盈亏情况．
先化简求值
,其中a＝－1，b＝
．
（本题满分16分,每题4分）
（1）计算：
（2）计算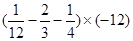
（3）解方程：
（4）解方程：
用圆规、直尺作图，不写作法，但要保留作图痕迹．
如图，已知线段m，n，求作线段AB，使AB=2m+n；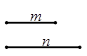
如图，直线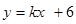
与x轴y轴分别相交于点E，F．点E的坐标（8,0）,点A的坐标为（6,0）。点P（x,y）是第一象限内的直线上的一个动点（点P不与点E，F重合）．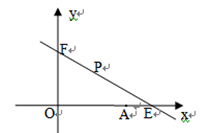
（1）求k的值；
（2）在点P运动的过程中，求出△OPA的面积S与x的函数关系式．
（3）若△OPA的面积为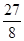
，求此时点P的坐标．