设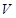 是已知平面
是已知平面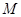 上所有向量的集合,对于映射
上所有向量的集合,对于映射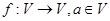 ,记
,记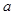 的象为
的象为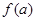 。若映射
。若映射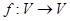 满足:对所有
满足:对所有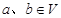 及任意实数
及任意实数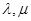 都有
都有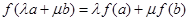 ,则
,则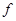 称为平面
称为平面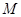 上的线性变换。现有下列命题:
上的线性变换。现有下列命题:
①设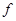 是平面
是平面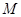 上的线性变换,
上的线性变换,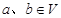 ,则
,则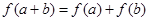 ;
;
②若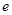 是平面
是平面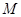 上的单位向量,对
上的单位向量,对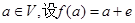 ,则
,则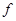 是平面
是平面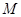 上的线性变换;
上的线性变换;
③对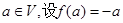 ,则
,则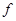 是平面
是平面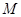 上的线性变换;
上的线性变换;
④设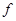 是平面
是平面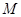 上的线性变换,
上的线性变换, ,则对任意实数
,则对任意实数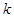 均有
均有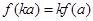 。
。
其中的真命题是 .(写出所有真命题的编号)
定义在R上的函数y=f(x)的图像经过坐标原点O,且它的导函数y=f¢(x)的图像是如图所示的一条直线,则y=f(x)的图像一定不经过第 象限.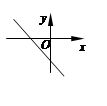
在平面直角坐标系xOy中,已知椭圆 的左焦点为F,直线x-y-1=0,x-y+1=0与椭圆分别相交于点A,B,C,D,则AF+BF+CF+DF=.
的左焦点为F,直线x-y-1=0,x-y+1=0与椭圆分别相交于点A,B,C,D,则AF+BF+CF+DF=.
已知圆柱的体积为16pcm3,则当底面半径r=cm时,圆柱的表面积最小.
“a=1”是“函数f(x)=x+acosx在区间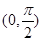 上为增函数”的条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空).
上为增函数”的条件(在“充要”、“充分不必要”、“必要不充分”、“既不充分又不必要”中,选择适当的一种填空).
已知函数f(x)=ex-ax在区间(0,1)上有极值,则实数a的取值范围是.