省《体育高考方案》于2012年2月份公布，方案要求以学校为单位进行体育测试，某校对高三1班同学按照高考测试项目按百分制进行了预备测试，并对50分以上的成绩进行统计，其频率分布直方图如图所示，若90～100分数段的人数为2人. 
(Ⅰ) 请估计一下这组数据的平均数M；
(Ⅱ) 现根据初赛成绩从第一组和第五组(从低分段到高分段依次为第一组、第二组、…、第五组)中任意选出两人，形成一个小组.若选出的两人成绩差大于20，则称这两人为“帮扶组”，试求选出的两人为“帮扶组”的概率.
已知函数
).
(Ⅰ) 若
，试确定函数
的单调区间；
(Ⅱ) 若函数在其图象上任意一点
处切线的斜率都小于
，求实数
的取值范围.
已知
的展开式中前三项的系数成等差数列．
（1）求n的值；（2）求展开式中的常数项；
从5名男同学与4名女同学中选3名男同学与2名女同学，分别担
任语文、数学、英语、物理、化学科代表．
(1)共有多少种不同的选派方法？
(2)若女生甲必须担任语文科代表，共有多少种不同的选派方法？
(3)若男生乙不能担任英语科代表，共有多少种不同的选派方法？
（本小题满分14分）已知：以点C (t, 
)(t∈R , t≠ 0)为圆心的圆与
轴交于点O, A，
与y轴交于点O, B，其中O为原点．
（Ⅰ）当t=2时，求圆C的方程；
（Ⅱ）求证：△OAB的面积为定值；
（Ⅲ）设直线y = –2x+4与圆C交于点M, N，若
，求圆C的方程．
本小题满分12分）已知实数
，
．
（Ⅰ）求点（a，b）在第一象限的概率；
（Ⅱ）求直线
与圆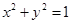
有公共点的概率．