如图所示,两块平行金属极板心MN水平放置,板长L="1" m,间距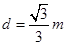 ,两金属板间电压
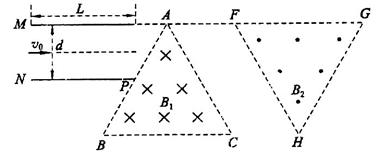
,两金属板间电压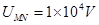 ;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场Bl,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上,B、C、H也处于同一直线上,AF两点距离为
;在平行金属板右侧依次存在ABC和FGH两个全等的正三角形区域,正三角形ABC内存在垂直纸面向里的匀强磁场Bl,三角形的上顶点A与上金属板M平齐,BC边与金属板平行,AB边的中点P恰好在下金属板N的右端点;正三角形FGH内存在垂直纸面向外的匀强磁场B2,已知A、F、G处于同一直线上,B、C、H也处于同一直线上,AF两点距离为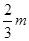 。现从平行金属极板MN左端沿中轴线方向入射一个重力不计的带电粒子,粒子质量
。现从平行金属极板MN左端沿中轴线方向入射一个重力不计的带电粒子,粒子质量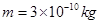 ,带电量
,带电量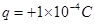 ,初速度
,初速度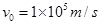 。
。
(1)求带电粒子从电场中射出时的速度v的大小和方向
(2)若带电粒子进入中间三角形区域后垂直打在AC边上,求该区域的磁感应强度Bl
(3)若要便带电粒子由FH边界进入FGH区域并能再次回到FH界面,求B2应满足的条件 。
如图所示,平面直角坐标系的y轴竖直向上,x轴上的 P点与 Q点关于坐标原点O对称,距离为2a.有一簇质量为m、带电量为+q的带电微粒,在xoy平面内,从P 点以相同的速率斜向上沿与x 轴正方向的夹角θ 方向射出,0°<θ<90°,经过某一个垂直于xoy平面向外、磁感应强度大小为 B的有界匀强磁场区域后,最终会聚到 Q 点,这些微粒的运动轨迹关于y 轴对称.为保证微粒的速率保持不变,需要在微粒的运动空间再施加一个匀强电场.重力加速度为g.求:
Q 点,这些微粒的运动轨迹关于y 轴对称.为保证微粒的速率保持不变,需要在微粒的运动空间再施加一个匀强电场.重力加速度为g.求:
(1)匀强电场场强E的大小和方向;
(2)若微粒在磁场中运动的轨道半径为a,求与x轴正方向成30°角射出的微粒从P 点运动到Q 点的时间t ;
(3)若微粒从P 点射出时的速率为v,试推出在x >0的区域中磁场的边界点坐标x 与y 应满足的关系式.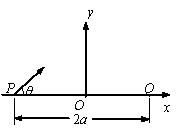
(15分)如图所示,一光滑斜面固定在水平面上,斜面上放置一质量不计的柔软薄纸带.现将质量为mA 的物体A 和质量mB 的物体B 轻放在纸带上.两物体可视为质点,物体初始位置数据如图所示,x1=1.6m,x2=3m.
(1)若纸带与物块间的动摩擦因数足够大,发现放在薄纸带上后 A、B两物体均静止在原 地,则mA 和mB 应满足什么关系?
地,则mA 和mB 应满足什么关系?
(2)若mA=2kg,mB=1kg,A与纸带间的动摩擦因数μA=0.5,B与纸带间的动摩擦因数μB=0.8,现将A、B两物体同时释放,求物体B 到达斜面底端的时间及两物体下滑过程中产生的摩擦热.(sin37°=cos53°=0.6,cos37°=sin53°=0.8)
一滑雪人与滑雪板的总质量为60kg,从长为100m、倾角为30°的斜坡顶端由静止开始匀加速下滑,经10s滑到了坡底。取g=10m/s2,求:
(1)滑雪人下滑的加速度;
(2)人与滑雪板所受的阻力(包括摩擦和空气阻力)。
一辆汽车原来匀速行驶,然后以2 m/s2的加速度加快行驶,从加快行驶开始,经12 s行驶了264 m,则;
(1)汽车在此12 s内的平均速度是多少?
(2)汽车开始加速时的初速度是多大?
神舟六号载人飞船在绕地球飞行了5 圈后变轨,轨道变为距地面高度为h的圆形轨道.已知地球半径为 ,地面附近的重力加速度为
,地面附近的重力加速度为 .求:
.求:
(1)飞船在圆轨道上运行的速度 ;
;
(2)飞船在圆轨道上运行的周期 .
.