已知抛物线的顶点在坐标原点,焦点为 ,点
,点 是点
是点 关于
关于 轴的对称点,过点
轴的对称点,过点 的直线交抛物线于
的直线交抛物线于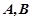 两点。
两点。
(Ⅰ)试问在 轴上是否存在不同于点
轴上是否存在不同于点 的一点
的一点 ,使得
,使得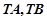 与
与 轴所在的直线所成的锐角相等,若存在,求出定点
轴所在的直线所成的锐角相等,若存在,求出定点 的坐标,若不存在说明理由。
的坐标,若不存在说明理由。
(Ⅱ)若 的面积为
的面积为 ,求向量
,求向量 的夹角;
的夹角;
在△ABC中,内角A,B,C所对边长分别为 ,
, ,
, ,
, .
.
(1)求 的最大值及
的最大值及 的取值范围;
的取值范围;
(2)求函数 的最大值和最小值.
的最大值和最小值.
已知集合A={x|x2-ax+a2-19=0},集合B={x|log2(x2-5x+8)=1},集合C={x|m =1,m≠0,|m|≠1}满足A∩B≠
=1,m≠0,|m|≠1}满足A∩B≠ ,A∩C=
,A∩C= ,求实数a的值;
,求实数a的值;
已知函数 ,其中a>0.
,其中a>0.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)若直线 是曲线
是曲线 的切线,求实数a的值;
的切线,求实数a的值;
(Ⅲ)设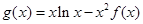 ,求
,求 在区间
在区间 上的最大值(其中e为自然对的底数)。
上的最大值(其中e为自然对的底数)。
已知各项均为正数的数列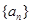 满足
满足 ,且
,且 ,其中
,其中 .
.
(Ⅰ)求数列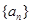 的通项公式;
的通项公式;
(Ⅱ)设数列 满足
满足 是否存在正整数m、n(1<m<n),使得
是否存在正整数m、n(1<m<n),使得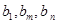 成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
成等比数列?若存在,求出所有的m、n的值,若不存在,请说明理由。
如图,在四棱锥P—ABCD中,ABCD为平行四边形,且BC⊥平面PAB,PA⊥AB,M为PB的中点,PA=AD=2.
(Ⅰ)求证:PD//平面AMC;
(Ⅱ)若AB=1,求二面角B—AC—M的余弦值。