如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2 A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.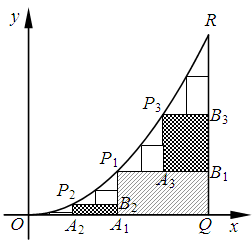
(I)求a2与an;
(Ⅱ)求Sn,并证明Sn<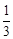 .
.
(本小题满分12 分)(注意:在试题卷上作答无效)
分)(注意:在试题卷上作答无效)
设定义在R上的函数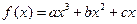 ,当时,f (x)取得极大值,并且函数
,当时,f (x)取得极大值,并且函数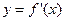 的图象关于y轴对称.(Ⅰ)求
的图象关于y轴对称.(Ⅰ)求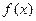 的表达式;(Ⅱ)若曲线
的表达式;(Ⅱ)若曲线 对应的解析式为
对应的解析式为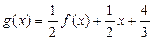 ,求曲线过点
,求曲线过点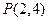 的切线方程.
的切线方程.
(本小题满分12分)(注意:在试题卷上作答无效)
在△ 中,角
中,角 、
、 、
、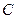 所对的边分别为
所对的边分别为 、
、 、
、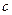 ,且
,且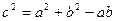 .
.
(Ⅰ)若 ,求角
,求角 ;
;
(Ⅱ)设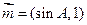 ,
, ,试求
,试求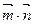 的取值范围.
的取值范围.
(本小题满分13分)
在数列{ 中,
中,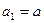 (
( 且
且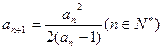
(1)求证 ;(2)求证
;(2)求证 ;
;
(3)若存在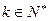 ,使得
,使得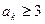 ,求证:
,求证:
(本小题满分13分)
已知曲线D: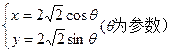 交
交 轴于A、B两点,曲线C是以AB为长轴,离心率
轴于A、B两点,曲线C是以AB为长轴,离心率 的椭圆。
的椭圆。
(1)求椭圆的标准方程;
(2)设M是直线 上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且
上的任一点,以OM为直径的圆交曲线D于P,Q两点(O为坐标原点)。若直线PQ与椭圆C交于G,H两点,交x轴于点E,且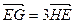 。试求此时弦PQ的长。
。试求此时弦PQ的长。
(本小题满分13分)
已知函数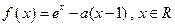 .
.
(1)若实数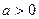 ,求函数
,求函数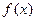 在
在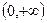 上的极值;
上的极值;
(2)记函数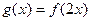 ,设函数
,设函数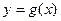 的图象C与
的图象C与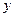 轴交于
轴交于 点,曲线C在
点,曲线C在 点处的切线与两坐标轴所围成的图形的面积为
点处的切线与两坐标轴所围成的图形的面积为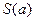 ,求当
,求当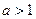 时
时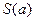 的最小值。
的最小值。