做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A,B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获毛利润分别为30元和40元,乙店铺获毛利润分别为27元和36元。某日王老板进货A款式服装35件,B款式服装25件。怎样分配给每个店铺各30件服装,使得在保证乙店铺毛利润不小于950元的前提下,王老板获取的总毛利润最大?最大的总毛利润是多少?
解不等式组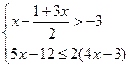 .
.
某工厂去年生产某种产品一件,所获取的利润率为59%,今年由于物价上涨,工厂生产这种产品的成本增加了6%,而今年与去年该产品的出厂售价一样,所以今年该工厂生产该产品一件所获取的利润率为 .
分式方程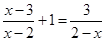 的解是 .
的解是 .
随着经济的发展,小新所在的公司每年都在一月份一次性的提高员工当年的月工资.小新2008年的月工资为2000元,在2010年时他的月工资增加到2420元,他2011年的月工资按2008到2010年的月工资的平均增长率继续增长.小新2011年的月工资为多少?
小新看了甲、乙两种工具书的单价,认为用自己2011年6月份的月工资刚好购买若干本甲种工具书和一些乙种工具书,当他拿着选定的这些工具书去付书款时,发现自己计算书款时把这两种工具书的单价弄对换了,故实际付款比2011年6月份的月工资少了242元,于是他用这242元又购买了甲、乙两种工具书各一本,并把购买的这两种工具书全部捐献给西部山区的学校.请问,小新总共捐献了多少本工具书?
如图,在单位长度为1的正方形网格中,一段圆弧经过格点A、B、C.请完成如下操作:
①以点O为原点、竖直和水平方向所在的直线为坐标轴、网格边长为单位长,建立平面直角坐标系;②画出该圆弧所在圆的圆心D的位置(不用写作法,保留作图痕迹),并连接AD、CD.请在(1)的基础上,完成下列问题:
①写出点的坐标:C _________(6,2)
、D ________;(2,0)
②⊙D的半径为________ 2 5
(结果保留根号);
③若扇形ADC是一个圆锥的侧面展开图,则该圆锥的侧面面积为 ____________5π4
(结果保留π);
④若E(7,0),试判断直线EC与⊙D的位置关系并说明你的理由.