在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).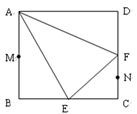
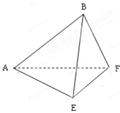
(Ⅰ)在三棱锥上标注出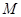 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ)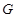 是线段
是线段 上一点,且
上一点,且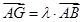 ,问是否存在点
,问是否存在点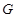 使得
使得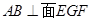 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
在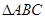 中,角
中,角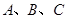 的对边分别为
的对边分别为 ,
,
且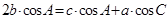 .
.
(1)求角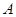 的大小;
的大小;
(2)若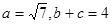 ,求
,求 的面积
的面积
设函数

(Ⅰ)若 ,
,
( i )求 的值; (ii)在
的值; (ii)在 。
。
(Ⅱ)当
 上是单调函数,求
上是单调函数,求 的取值范围。(参考数据
的取值范围。(参考数据
如图所示,四边形ABCD是边长为1的正方形,MD⊥平面ABCD,NB⊥平面ABCD,且MD=NB=1,E为BC的中点.
(1)求异面直线NE与AM所成角的余弦值;
(2)在线段AN上是否存在点S,使得ES⊥平面AMN?若存在,求线段AS的长;若不存在,请说明理由.
已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,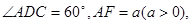 (I)求证:AC⊥BF;
(I)求证:AC⊥BF;
(II)若二面角F—BD—A的大小为60°,求a的值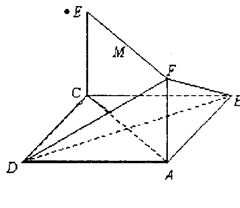
已知 为实数,
为实数, (1)求导数
(1)求导数 ;(2)若
;(2)若 ,求
,求 在
在 上的最大值和最小值
上的最大值和最小值