电子蛙跳游戏是:青蛙第一步从如图所示的正方体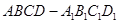 顶点
顶点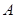 起跳,每步从一顶点跳到相邻的顶点.
起跳,每步从一顶点跳到相邻的顶点.
(1)求跳三步跳到 的概率
的概率 ;
;
(2)青蛙跳五步,用 表示跳到过
表示跳到过 的次数,求随机变量
的次数,求随机变量 的概率分布及数学期望
的概率分布及数学期望 .
.
已知 、
、 、
、 为
为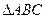 的三个内角,且其对边分别为
的三个内角,且其对边分别为 、
、 、
、 ,若
,若

(1)求角 的值;
的值;
|
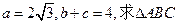 的面积.
的面积.
已知变量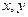 满足
满足 则
则 的最小值是.
的最小值是.
(本题满分14分)数列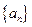 满足
满足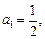
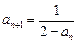 .
.
(1)求数列{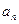 }的通项公式;(2)设数列{
}的通项公式;(2)设数列{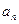 }的前
}的前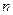 项和为
项和为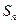 ,证明
,证明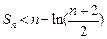 .
.
(本题满分14分)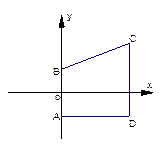
在梯形ABCD中,AB⊥AD,AB∥CD,A、B是两个定点,其坐
标分别为(0,-1)、(0,1),C、D是两个动点,且满足|CD|=|BC|.
(1)求动点C的轨迹E的方程;
(2)试探究在轨迹E上是否存在一点P?使得P到直线y=x-2的
距离最短;
(3)设轨迹E与直线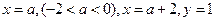 所围成的图形的
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
(本小题满分12分)
2008年北京奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌,保守估计中国乒乓球男队获得每枚金牌的概率均为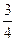 ,中国乒乓球女队获得每枚金牌的概率均为
,中国乒乓球女队获得每枚金牌的概率均为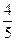 .
.
(1)求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;
(2)记中国乒乓球队获得金牌的数为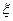 ,按此估计
,按此估计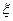 的分布列和数学期望
的分布列和数学期望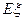 。
。