如图,已知斜坡AB长60米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
(1)若修建的斜坡BE的坡角(即∠BEF)不大于45°,则平台DE的长最多为多少米?
(2)一座建筑物GH距离坡角A点27米远(即AG=27米),小明在D点测得建筑物顶部H的仰角(即∠DHM)为30°,点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
为迎接建党100周年,某校组织学生开展了党史知识竞赛活动.竞赛项目有: .回顾重要事件; .列举革命先烈; .讲述英雄故事; .歌颂时代精神.学校要求学生全员参加且每人只能参加一项,为了解学生参加竞赛情况,随机调查了部分学生,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中信息解答下列问题:

(1)本次被调查的学生共有 名;
(2)在扇形统计图中" 项目"所对应的扇形圆心角的度数为 ,并把条形统计图补充完整;
(3)从本次被调查的小华、小光、小艳、小萍这四名学生中,随机抽出2名同学去做宣讲员,请用列表或画树状图的方法求出恰好小华和小艳被抽中的概率.
先化简,再求值: ,其中 .
课本再现
(1)在证明"三角形内角和定理"时,小明只撕下三角形纸片的一个角拼成图1即可证明,其中与 相等的角是 ;

类比迁移
(2)如图2,在四边形 中, 与 互余,小明发现四边形 中这对互余的角可类比(1)中思路进行拼合:先作 ,再过点 作 于点 ,连接 ,发现 , , 之间的数量关系是 ;
方法运用
(3)如图3,在四边形 中,连接 , ,点 是 两边垂直平分线的交点,连接 , .
①求证: ;
②连接 ,如图4,已知 , , ,求 的长(用含 , 的式子表示).

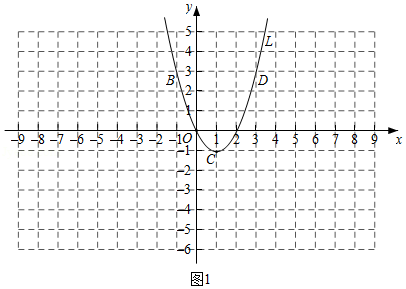
二次函数 的图象交 轴于原点 及点 .
感知特例
(1)当 时,如图1,抛物线 上的点 , , , , 分别关于点 中心对称的点为 , , , , ,如表:
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
①补全表格;
②在图1中描出表中对称后的点,再用平滑的曲线依次连接各点,得到的图象记为 .
形成概念
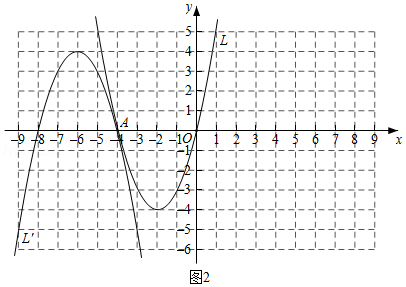
我们发现形如(1)中的图象 上的点和抛物线 上的点关于点 中心对称,则称 是 的“孔像抛物线”.例如,当 时,图2中的抛物线 是抛物线 的“孔像抛物线”.
探究问题
(2)①当 时,若抛物线 与它的“孔像抛物线” 的函数值都随着 的增大而减小,则 的取值范围为 ;
②在同一平面直角坐标系中,当 取不同值时,通过画图发现存在一条抛物线与二次函数 的所有“孔像抛物线” 都有唯一交点,这条抛物线的解析式可能是 (填“ ”或“ ”或“ ”或“ ”,其中 ;
③若二次函数 及它的“孔像抛物线”与直线 有且只有三个交点,求 的值.
如图1,四边形 内接于 , 为直径,点 作 于点 ,连接 .
(1)求证: ;
(2)若 是 的切线, ,连接 ,如图2.
①请判断四边形 的形状,并说明理由;
②当 时,求 , 与 围成阴影部分的面积.
