在四棱锥P-ABCD中，侧面PCD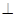
底面ABCD，PD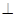CD，底面ABCD是直角梯形，AB∥DC，
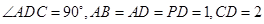ADC-900,AB=AD=PD=1.CD=2.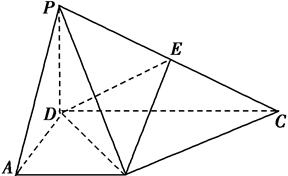
(I)求证：BC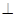平面PBD：
(II)设E为侧棱PC上异于端点的一点，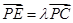
，试确定
的值，使得二面角
E-BD-P的大小为
．
某企业在第1年初购买一台价值为120万元的设备M，M的价值在使用过程中逐年减少，从第2年到第6年，每年初M的价值比上年初减少10万元；从第7年开始，每年初M的价值为上年初的75%．
（1）求第n年初M的价值
的表达式；
（2）设
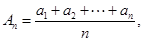若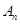
大于80万元，则M继续使用，否则须在第n年初对M更新，
证明：第6年初仍可对M继续使用．
已知数列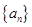
前
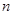项和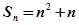
（1）求数列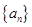的通项公式；
（2）令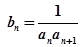
，求证：数列{
}的前n项和
.
已知数列
的首项
，通项
（
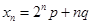为常数），且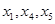
成等差数列.
（1）求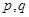
的值；
（2）数列的前
项的和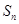
.
已知在公比为实数的等比数列
中，
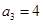，且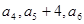
成等差数列．
(1) 求数列的通项公式；
(2) 设数列的前n项和为Sn，求S10.
已知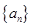
是等差数列，其中
.
（1）求数列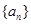
的通项公式；
（2）求
值.