某市在市内主干道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为O,半径为100m,并与北京路一边所在直线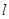 相切于点M.A为上半圆弧上一点,过点A作
相切于点M.A为上半圆弧上一点,过点A作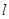 的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位:
的垂线,垂足为B.市园林局计划在△ABM内进行绿化.设△ABM的面积为S(单位: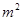 ),
), (单位:弧度).
(单位:弧度).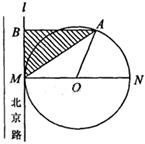
(I)将S表示为 的函数;
的函数;
(II)当绿化面积S最大时,试确定点A的位置,并求最大面积.
(本小题12分)
正△ABC的边长为4,CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A—DC—B.
(Ⅰ)试判断直线AB与平面DEF的位置关系,并说明理由;
(Ⅱ)求直线BC与平面DEF所成角的余弦值;
(Ⅲ)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论.
(本小题15分)
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
(1)证明:D1E⊥A1D ;
(2)当E为AB的中点时,求点E到面ACD1的距离;
(3)AE等于何值时,二面角D1-EC-D的大小为 .
.
(本小题10分)
设 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量 ,向量
,向量 ,
, ,动点
,动点 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)点 为当
为当 时轨迹E上的任意一点,定点
时轨迹E上的任意一点,定点 的坐标为(3,0),
的坐标为(3,0),
点 满足
满足 ,试求点
,试求点 的轨迹方程。
的轨迹方程。
(本小题10分)
某隧道的横段面是由一段抛物线及矩形的三边组成的,尺寸如图所示。某卡车空车时能通过此隧道。现载一集装箱,箱宽3米,车与箱共高 米。此时,卡车能否通过此隧道?说明理由。
米。此时,卡车能否通过此隧道?说明理由。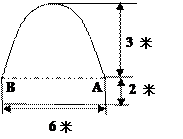
已知焦点在x轴上,中心在坐标原点的椭圆C的离心率为 ,且过点
,且过点 .
.
(I)求椭圆C的方程;
(II)直线 分别切椭圆C与圆
分别切椭圆C与圆 (其中3<R<5)于A、B两点,求|AB|的最大值.
(其中3<R<5)于A、B两点,求|AB|的最大值.