如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径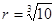 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.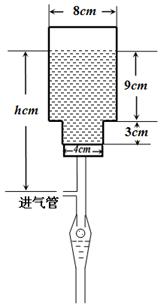
(1)如果瓶内的药液恰好 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为 (单位:厘米),已知当
(单位:厘米),已知当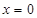 时,
时, .试将
.试将 表示为
表示为 的函数.(注:
的函数.(注: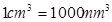 )
)
如图所示几何体是一棱长为4 cm的正方体,若在它的各个面的中心位置上,各打一个直径为2 cm、深为1 cm的圆柱形的孔,求打孔后几何体的表面积是多少?(π=3.14) 
直平行六面体的底面为菱形,过不相邻两条侧棱的截面面积分别为Q1、Q2,求它的侧面积. 
一个正三棱台的上、下底面边长分别是3 cm和6 cm,高是 cm.(1)求三棱台的斜高;(2)求三棱台的侧面积与表面积.
cm.(1)求三棱台的斜高;(2)求三棱台的侧面积与表面积.
正三棱柱ABC—A1B1C1的底面正△ABC的外接圆半径为 ,它的侧棱长为8,求正三棱柱的侧面积.
,它的侧棱长为8,求正三棱柱的侧面积.
如图所示棱锥P—ABCD中,底面ABCD是正方形,边长为a,PD=a,PA=PC= ,且PD是四棱锥的高.
,且PD是四棱锥的高. 
(1)在这个四棱锥中放入一个球,求球的最大半径;
(2)求四棱锥外接球的半径.