设函数f(x)= 在[1+,∞
在[1+,∞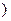 上为增函数.
上为增函数.
(1)求正实数a的取值范围.
(2)若a=1,求征: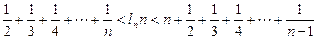 (n∈N*且n≥2)
(n∈N*且n≥2)
已知正项数列 的前
的前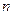 项和
项和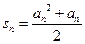 ,
,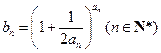 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)定理:若函数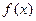 在区间D上是凹函数,且
在区间D上是凹函数,且 存在,则当
存在,则当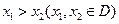 时,总有
时,总有 .请根据上述定理,且已知函数
.请根据上述定理,且已知函数 是
是 上的凹函数,判断
上的凹函数,判断 与
与 的大小;
的大小;
(Ⅲ)求证: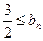 .
.
已知 函数f(x)=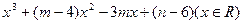 的图像关于原点对称,其中m,n为实常数。
的图像关于原点对称,其中m,n为实常数。
(1)求m , n的值;
(2)试用单调性的定义证明:f (x) 在区间[-2, 2] 上是单调函数;
(3)[理科做] 当-2≤x≤2 时,不等式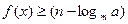 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
已知实数x满足 求函数
求函数 |的最小值。
|的最小值。
已知函数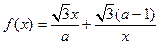 (
(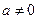 且
且 ).
).
(1) 试就实数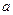 的不同取值,写出该函数的单调递增区间;
的不同取值,写出该函数的单调递增区间;
(2) 已知当 时,函数在
时,函数在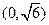 上单调递减,在
上单调递减,在 上单调递增,求
上单调递增,求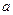 的值并写出函数的解析式;
的值并写出函数的解析式;
(3) (理)记(2)中的函数的图像为曲线 ,试问是否存在经过原点的直线
,试问是否存在经过原点的直线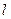 ,使得
,使得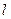 为曲线
为曲线 的对称轴?若存在,求出
的对称轴?若存在,求出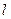 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(文) 记(2)中的函数的图像为曲线 ,试问曲线
,试问曲线 是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.
是否为中心对称图形?若是,请求出对称中心的坐标并加以证明;若不是,请说明理由.