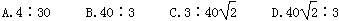如图所示，竖直平面内的轨道ABCD由水平轨道AB与光滑的四分之一圆弧轨道CD组成，AB恰与圆弧CD在C点相切，轨道固定在水平面上。一个质量为m的小物块（可视为质点）从轨道的A端以初动能Ek0冲上水平轨道AB，沿着轨道运动，由DC弧滑下后停在水平轨道AB的中点。已知水平轨道AB长为L。则：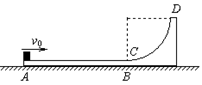
A．小物块与水平轨道的动摩擦因数 |
B．为了保证小物块不从轨道的D端离开轨道，圆弧轨道的半径R应满足 |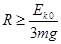
C．如果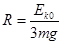 ，且增大小物块的初动能，使得小物块冲上轨道后可以达到最大高度是1.5R，则小物块将滑离水平轨道 |
| D．如果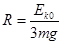，且增大小物块的初动能，使得小物块冲上轨道后可以达到最大高度是2R，则小物块将滑离水平轨道 |
如图所示,一理想变压器原副线圈匝数比为4:1,图中
五只电灯完全相同,若B、C、D、E都能正常发光，则A灯（）
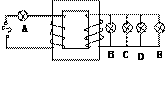
A .一定能正常发光 B .比正常发光暗
C .比正常发光亮 D .一定被烧坏
如图13-4-4（a）是电热毯的电路图，电热丝接在u=311sin100πtV的电源上，被加热到一定温度后，通过装置P使输入电压变为如图13-4-4（b）所示的波形，从而进入保温状态若电热丝的电阻R保持不变，此时交流电压表的示数是（）
| A．100V | B．155.5V |
| C．220V | D．311V |
一只电饭煲和一台洗衣机同时并入u=311sin314tV的交流电源上，均正常工作，用电流表分别测得电饭煲的电流是5A；洗衣机的电流是0.5A，下列说法正确的是（ ）
| A．电饭煲的电阻是44Ω，洗衣机电动机线圈电阻是440Ω |
| B．电饭煲消耗的功率为1555W，洗衣机电动机消耗的功率为155.5W |
| C．1分钟内电饭煲消耗的电能为6.6×104J，洗衣机电动机消耗的电能为6.6×103J |
| D．电饭煲发热功率是洗衣机电动机发热功率的10倍 |
同步卫星轨道半径为r，运行速率为v1，加速度为a1；地球赤道上的物体随地球自转的向心加速度为a2；第一宇宙速度为v2；地球半径为R。则下列关系式正确的是( )
理想变压器的原线圈接入表达式为i＝Imsinωt的交变电流，一只灯泡和交流电流表串联后接在副线圈两端，读数为0.4 A，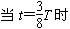
，原线圈的电流i＝30 mA，由此可知，此变压器的原副线圈匝数之比为( )