如图所示，一光滑绝缘圆管轨道位于竖直平面内，半径为0.2m。以圆管圆心O为原点，在环面内建立平面直角坐标系xOy，在第四象限加一竖直向下的匀强电场，其他象限加垂直于环面向外的匀强磁场。一带电量为+1.0C、质量为0.1kg的小球（直径略小于圆管直径），从x坐标轴上的b点由静止释放，小球刚好能顺时针沿圆管轨道做圆周运动。（重力加速度g取10m/s2）
（1）求匀强电场的电场强度E；
（2）若第二次到达最高点a时，小球对轨道恰好无压力，求磁感应强度B ；
（3）求小球第三次到达最高点a时对圆管的压力。
如图甲所示，在水平面上固定有长为L=2m、宽为d=1m的金属“U”型轨导，在“U”型导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场，且磁感应强度随时间变化规律如图乙所示。在t=0时刻，质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动，导体棒与导轨之间的动摩擦因数为μ=0.1，导轨与导体棒单位长度的电阻均为λ=0.1Ω/m，不计导体棒与导轨之间的接触电阻及地球磁场的影响（取g=10m/s2）。
（1）通过计算分析4s内导体棒的运动情况；
（2）计算4s内回路中电流的大小，并判断电流方向；
（3）计算4s内回路产生的焦耳热。
滑雪者能在软绵绵的雪地上高速奔驰，是因为白雪里充满了空气，当滑雪板压在雪地上时会把雪地里的空气逼出来，在滑雪板与雪地间形成一个暂时的气垫，从而大大的减少了雪地对滑雪板的摩擦。然而，当滑雪板的速度相对雪地的速度较小时，与雪地接触的时间超过某一值就会陷下去，使他们的摩擦增大。
假设滑雪者的速度超过4m/s时，滑雪板与雪地间的动摩擦因数就会由0.25变为0.125。一个滑雪者从倾角为θ = 37°的坡顶A由静止开始自由下滑，滑至坡底B后，又滑上一段水平雪地，最后停在C处，如图。不计空气阻力，坡长为LAB =26m，取g=10m/s2，sin37°=0.6，cos37°=0.8，求滑雪者从静止开始到动摩擦因数发生变化经历的时间；
滑雪者到达B处的速度；
滑雪者在水平雪地上运动的最大距离。
已知锌的逸出功W0="3.34" eV，试通过计算说明：用波长λ=0.2μm的光照射锌板时能否发生光电效应。(普朗克常量h=6.63×10－34 J·s，真空中光速c=3×108m/s)
如图所示，半圆玻璃砖的半径R=10cm，折射率为n=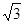
，直径AB与屏幕垂直并接触于A点。激光a以入射角i =30°射向半圆玻璃砖的圆心O，结果在水平屏幕MN上出现两个光斑。求两个光斑之间的距离L。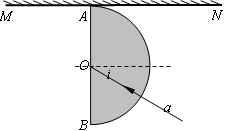
两个同学利用假期分别去参观北京大学和南京大学的物理实验室，各自在那里利用先进的DIS系统较准确地探究了“单摆的周期T与摆长L的关系”，他们通过校园网交换实验数据，并由计算机绘制了T2～L图象，如图甲所示．去北大的同学所测实验结果对应的图线是▲（选填“A”或“B”）。另外，在南大做探究的同学还利用计算机绘制了两种单摆的振动图象（如图乙），由图可知，两单摆摆长之比
▲。