如图,已知△ABC中,∠B="90" º,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
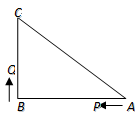
(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间(只要直接写出答案).
由于受到手机更新换代的影响,某手机店经销的Iphone4手机二月售价比一月每台降价500元.如果卖出相同数量的Iphone4手机,那么一月销售额为9万元,二月销售额只有8万元.
(1)一月Iphone4手机每台售价为多少元?
(2)为了提高利润,该店计划三月购进Iphone4s手机销售,已知Iphone4每台进价为3500元,Iphone4s每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)该店计划4月对Iphone4的尾货进行销售,决定在二月售价基础上每售出一台Iphone4手机再返还顾客现金a元,而Iphone4s按销售价4400元销售,如要使(2)中所有方案获利相同,a应取何值?
如图,正比例函数 的图象与反比例函数
的图象与反比例函数
 在第一象限的图象交于
在第一象限的图象交于 点,过
点,过 点作
点作 轴的垂线,垂足为
轴的垂线,垂足为 ,已知
,已知 的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
的面积为1,点B(-1,t)为反比例函数在第三象限图象上的点.
(1)求反比例函数的解析式;
(2)试求出点A、点B的坐标;
(3)在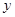 轴上求一点
轴上求一点 ,使
,使 的值最大.
的值最大.
某市进行“百万家庭低碳行,垃圾分类要先行”的活动,为了了解该市此项活动的开展情况,某调查统计公司准备采用以下调查方式中的一种进行调查:
A、从一个社区随机选取1000名居民;
B、从一个城镇的不同住宅楼中随机选取1000名居民;
C、从该市公安局户籍管理处随机选取1000名城乡居民作为调查对象,然后进行调查。
(1)在上述调查方式中,你认为比较合理的一个是____________(填序号)。
(2)由一种比较合理的调查方式所得到的数据制成了如图的条形图、扇形图.
①图2中所缺少的百分数是____________;
②这次随机调查中,公民年龄的中位数所在年龄段是______________(填写年龄段);
③这次随机调查中,年龄段是“25岁以下”的公民中“不赞同”的有5名,它占“25岁以下”人数的百分数是_____________;
④如果把所持态度中的“很赞同”和“赞同”统称为“支持”,那么这次被调查公民中“支持”的人有__________
如图, 、
、 、
、 、
、 四点在一直线上,
四点在一直线上, ,
, ∥
∥ ,且
,且 .
.
求证:(1) ≌
≌ ;(2)
;(2) .
.
(1)计算: ;(2)解不等式组:
;(2)解不等式组: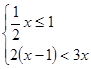 .
.